Mathematical Arguments: 6.0

• Indicator of Progress
• Teaching Strategies

Supporting materials

• Related Progression Points
• Developmental Overview of Working Mathematically (PDF - 31Kb)
• Developmental Overview of Structure (PDF - 35Kb)
• Developmental Overview of Space (PDF - 32Kb)

Indicator of Progress

Students are able to follow simple steps of deductive reasoning that combine together to make a formal proof. This is achieved as a culmination of work at earlier levels where students will have built up the following understandings:

• recognising the need for proof
• recognising the important role that specific examples play in testing the truth of conjectures and giving insight into why a result might be true
• recognising that a generalisation about an infinite number of cases cannot be proved by showing specific examples
• following arguments with an increasing number of steps
• identifying gaps in reasoning
• increasingly using algebra to express generality
• appreciating basic logical structures of deduction and the need to work from clear definitions.

More about deductive reasoning.

 

Illustration 1: Recognising a special case of a property

Students working at this level should be able to explain some angle properties of circles in terms of properties of triangles, such as showing angle at centre is twice angle at circumference by constructing isosceles triangles.

Students will be able to make further deductions from this property. For example, they will be able to show that the angle in a semi-circle is a right angle.

The diagram on the left shows an angle at the centre <AOC, which is twice the angle at the circumference <ABC. The diagram on the right is a special case of the diagram on the left, where the angle at the centre <A'OC' is a straight angle (on the diameter). The angle at the circumference <A'B' C' is therefore half of 180 degrees, that is, 90 degrees. So the proof that the angle in a semicircle is a right angle follows directly from the proof that the angle at the centre is twice the angle at the circumference.

 

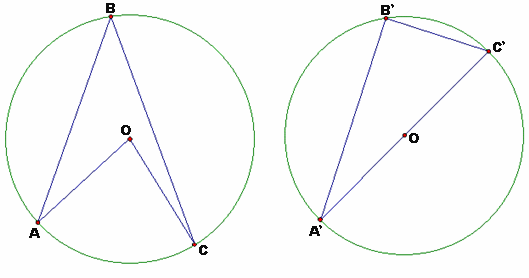
Illustration 2: Following an argument using algebra

Students will be able to follow a formal proof such as the following. In this proof, the algebraic manipulation is straight forward. It is the interpretation that is most challenging, especially expressing the consecutive numbers in terms of n and connecting the algebraic form 3(n +1) with being a multiple of 3.

Proposition:

The sum of 3 consecutive natural numbers is divisible by 3.

Proof:

Let n be any natural number. The next two consecutive natural numbers are (n + 1) and (n + 2).

The sum of the three consecutive natural numbers is:
S = n + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1)

This shows that the sum, S, is 3 times a natural number (namely (n +1)) and hence S is exactly divisible by 3. This proof works for all natural numbers n.

 

Illustration 3: Extending an argument

Students who can follow an argument will be able to make simple extensions of it. For example, having shown that the sum of three consecutive integers is divisible by 3 (see above), can we say that the sum of any four consecutive integers is divisible by 4?

Let the four integers be n, n + 1, n + 2 and n + 3.
Then S= n + (n + 1) + (n + 2) + (n + 3) = 4n + 6

Students will be able to show by numerical counter-examples and also by algebra, that this sum is never divisible by 4.

Is the sum of 5 consecutive integers divisible by 5? What about 6 consecutive integers? What is the generalisation?

 

Teaching Strategies

Teaching students to follow formal mathematical arguments requires that teachers demonstrate some formal arguments, and also that they engage students in conjecturing activities to develop an appreciation of the need for proof. Some important strategies are:

• Illustrating proofs with examples
• Involving students in investigation and discovery before offering proofs
• Leading students through simple proofs that they may have met previously, making sure they recognise the logical reasoning that is used at each stage
• Extending proofs, illustrating with examples students have met before. Students will find it easier to construct a simple extension to a proof rather than construct an entire proof
• Completing a proof, by including the justifications for each step of reasoning
• Asking students for examples to illustrate a general step in a specific way
• Filling in missing steps of reasoning
• Taking every opportunity to present mathematics as a subject that explains why.

Activity 1: Completing an argument uses a series of structured steps, to lead students through a proof of Pythagoras’ theorem.
Activity 2 and Activity 3 both present number properties that can be conjectured by students and proved with algebra.

 

Activity 1: Completing an argument

In this activity students are provided with a series of structured steps to lead them through a proof of Pythagoras’ theorem. There are many wonderful proofs of Pythagoras' theorem. This proof uses algebra appropriate for students at this level. This is provided as an example of a teaching activity that assists students to engage with proof in an active way. The student resource sheet can be downloaded here: Proving Pythagoras' Theorem (PDF - 22Kb).

 

Activity 2: Proving with algebra

There is a special trick for squaring numbers that are something and a half . For example, to square six and a half, you multiply 6 by 7 (i.e. by one greater) and add a quarter. The prediction can be checked by normal multiplication. Here is another example and then an algebraic generalisation. In order to prove that this special trick always works we have to prove that the last statement is true for all numbers using algebra.

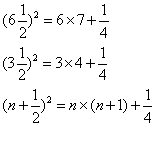Proof

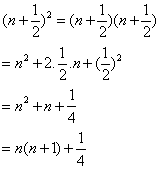
Creating the algebraic generalisation that needs to be proved, is likely to be more challenging than carrying out the algebraic manipulation. To assist students in creating such an algebraic generalisation for themselves, and in interpreting one that is given to them, teachers can:

• make sure that students use several specific values of n to check what the statement is saying numerically
• encourage students to translate step by step from the general observation about squaring to the algebraic statement, not to try to do it in one step. Students should express each of the following in terms of one variable: the number and a half, the number one greater, and the product.

Extension: the square of the average or the average of the squares

6 ¹/₂ is half way between 6 and 7 (i.e. it is the average of 6 and 7).

Is (6 ¹/₂)² half way between 6² and 7²? (i.e. is it the average of 6² and 7²?)

No! The square of the average is 1/4 less than the average of the squares.

Algebra can show that this always works.

 

Activity 3: Proving conjectures about number patterns

Algebra is an important tool for proving general statements. It transcends specific numerical examples, to provide general reasoning. As well as being able to do the required symbolic manipulation, students need to understand what the symbols mean in the context of the problem. They also need to be able to express mathematical relationships in algebraic language and be able to interpret algebraic results in the context of the problem.

There are four examples below, requiring different levels of algebraic skill. Some students will be able to prove these themselves; others will be able to follow the argument presented by others.

The instructions for each pattern are the same.
1. Check that these numerical statements are correct.
2. Observe and describe the pattern verbally.
3. Write down the next three numerical statements in the pattern and show that they are true.
4. If the numerical checks show that your pattern is likely to be correct, then prove that your pattern holds true for all numbers using algebra. If the numerical checks do not support the pattern, go back to step 2.

Pattern 1	Pattern 2	Pattern 3	Pattern 4
1 × 3 + 1 = 2² 2 × 4 + 1 = 3² 3 × 5 + 1 = 4²		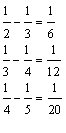	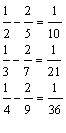1² + 2² + 2² = 3² 2² + 3² + 6² = 7² 3² + 4² + 12² = 13²

The algebraic generalisations are:

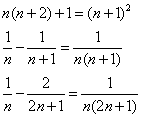n² + (n + 1)² + [n(n + 1)]² = [n(n + 1) + 1]²