Mathematical Deductions: 5.0

Indicator of Progress
Teaching Strategies

Supporting materials

Indicator of Progress

Students are able to follow simple steps of deductive reasoning.

At every level, students need to follow steps of deductive reasoning. Students cannot learn mathematics without learning 'why'. By this stage, students are becoming more able to recognise the links between logically connected statements. Prior to this, they may accept that each individual statement in a logical argument is true, but not see how successive statements build onto previous statements to make a chain of reasoning. Sometimes this may be due to lack of knowledge of mathematical properties.

Illustration 1: Concepts and vocabulary

Students who do not have the necessary mathematical vocabulary are often unable to explain their reasoning. “I know it’s true – it just has to be, but I can’t explain it” or “I don’t know the right words.” The opportunity to practise the use of correct mathematical language is essential so that students are able to justify their reasoning.

Students who can follow an argument will be able to make simple extensions of it.

For example, when they have seen how algebra can be used to prove some simple cases in Activities 4, 5 and 6 below, they will be able to adapt it to other cases, where the same general principles apply.

Teaching Strategies

Teaching strategies to strengthen students' deductive reasoning include:

using investigations and conjecturing to highlight the need to be sure that something is always true
presenting simple arguments for students to complete (e.g. by filling in reasons)
getting students to 'recycle' arguments in slightly different situations so that they can re-use reasoning patterns (this is an excellent method of active reflection on what has been learned)
constantly checking deductive steps against examples
taking every opportunity to make mathematics a 'why' subject, not just a 'what' and 'how' subject.

Activity 1: Investigations motivate deductive reasoning shows how deduction needs to be based in exploration of actual examples (Space context).
Activity 2: Providing missing reasons uses the same parallelogram investigation to illustrate how students can be set tasks to fill in gaps in reasoning.
Activity 3: Proving divisibility tests by algebra takes a well known fact and proves it for 2-digit numbers and suggests that students extend the proof beyond this.
Activity 4 (a number curiosity)
Activity 5 (conjecturing about calendar patterns) and
Activity 6 (generalising) adopt similar approaches to deduction using algebra.

Activity 1: Investigations motivate deductive reasoning

Deductive reasoning is essential to mathematics in order to establish that something that appears to be true (from considering several cases and where there is an infinite number of cases) is always true. For example, there is an infinite number of parallelograms. By definition, they all have two pairs of parallel sides. Do they all have opposite angles equal and opposite sides the same length? A few examples cannot be convincing.

A first step is to motivate students to want to find out if a statement is always true. They need to explore the situation and, if possible discover some of the facts for themselves. Students then need to consider whether the statement is always true.

Students can do this with pencil and paper. However, interactive geometry software such as The Geometer’s Sketchpad or Cabri Geometry is particularly appropriate for conjecturing activities in geometry. The dynamic imagery associated with these software environments enables students to measure quantities and to develop and test conjectures based on these observations. This sets the scene for deduction.

The diagram below shows measurements made from a dynamic geometry file. The vertices of hthe parallelogram can be dragged, with measurements being constantly updated.

Activity 2: Providing missing reasons

Students who can follow a logical argument will be able to give reasons for the steps and be able to fill in some missing steps. A good teaching strategy is to give students a partially completed argument and have them fill in the reasons, as in the example below.

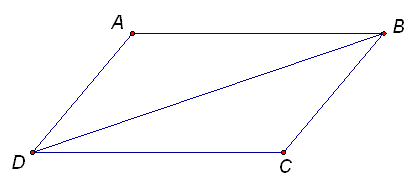
Example 1: Proving that the opposite angles of a parallelogram are equal

Copy and complete the proof.

ABCD is a parallelogram. By definition, both pairs of opposite sides are parallel. We can prove that both pairs of opposite angles are also equal.

In triangles ABD and CDB:

angle ABD = angle BDC
How do we know this? Student to fill in reason.
angle ADB = angle CBD
How do we know this? Student to fill in reason.
So angle ADC = angle ABC
How do we know this? Student to fill in reason.
Also angle DAB = angle BCD
How do we know this? Student to fill in reason.

In this argument, no justification has been given for the statements such as angle ABD = angle BDC. Students should be able to give a reason (eg that AB || DC and BD is a transversal, so the alternate angles, angle ABD and angle BDC are equal).

To show that angle DAB = angle BCD, students can say that if two angles of one triangle are equal to two angles of a second triangle then the third angles of the triangles must be equal.

Example 2: Proving that the opposite sides of a parallelogram are equal

Copy and complete the proof.

ABCD is a parallelogram. By definition both pairs of opposite sides are parallel. We can prove that both pairs of opposite sides are also equal.

In triangles ABD and CDB:

angle ABD = angle BCD
How do we know this? Student to fill in reason.
angle ADB = angle ….
How do we know this? Student to fill in reason.
BD is common to both triangles.
So AD = BC and AB = DC
How do we know this? Student to fill in reason.

The reasons here depend on alternate angles and also on showing that two triangles are congruent.

Activity 3: Proving divisibility tests by algebra

Algebra is an important tool for proving general statements. It transcends specific numerical examples, to provide general reasoning. As well as being able to do the required symbolic manipulation, students need to understand what the symbols mean in the context of the problem. They also need to be able to express mathematical relationships in algebraic language and be able to interpret algebraic results in the context of the problem.

This activity illustrates how some facts about numbers, known from earlier years, can be proved at this level. In addition, students will be able to demonstrate that they can follow the argument, by extending it.

Divisibility tests for 3 and 9

Students can rediscover (if needed) the tests for divisibility by 3 and by 9. If the digits add to a multiple of 3 (or 9) the number will also divide by 3 (or 9). In the past, we have learned this as a fact on authority, and tested some examples. How do we know it is always true? Are there counter-examples? (No.) But we have not tested all possible cases. So we should attempt to prove it.

Student need to use the language of algebra, and need to remember the way numbers use place value. Students show the value of the tens digit by 10a , and the ones digit by b, since the digits may be different.

Then a two-digit number is, in general, 10a + b. Rewrite it as 9a + what? Check that the answer makes sense with values of a and b.

Try some examples: if (a + b) is 5, will the number divide by 3 or 9?

The result will be divisible by 9 if (a + b) is divisible by 9, and the same for divisible by 3.

Extension

Ask students to extend the proof to 3 and 4 digit numbers. We can express any 3-digit number as

100a + 10b + c. This can be rewritten as 99a + 9b + (a + b + c) = 9(11a + b) + (a + b + c).

Activity 4: Proving and extending a number curiosity

Ask students to write down any two-digit number. Reverse the digits and write the larger above the smaller. Subtract. There are two things to discover about the answers you get. Spend some time exploring examples and conjecturing at this point.

Students will find that the answers are always multiples of 9 and that the particular multiple of 9 is given by the difference between the two digits in the number. So far it is a conjecture. Further testing will reveal that it always works, even when the digits are the same (where the answer is 9 × 0).

So why is it so? We need the language of algebra again, with the same ideas as above.

If the first number is 'ab' (ie the tens digit is a and the ones digit is b), then the starting number will be equal to 10a + b, and the reverse will be equal to 10b + a.

Let us assume that a is greater than or equal to b.

So the subtraction is:

10a + b – (10b + a) = 10a + b – 10b – a = 9a – 9b = 9(a – b)

Discuss with students that this result means - it is a multiple of 9 and it is the product of 9 and the difference between a and b. To make sense of this, many students will need to follow what happens with numbers.

Example: 53 – 35, so a = 5 and b = 3. The answer is 18, which is 9 × 2.

10 × 5 + 3 – (10 × 3 + 5) = 10 × 5 + 3 – 10 × 3 – 5 = 9 × 5 – 9 × 3 = 9 × (5 – 3) = 9 × 2 = 18

Extension

Many students will be able to extend this argument to three digits (using a , b and c).

Activity 5: Calendar patterns

On a calendar, such as the one shown, select any four numbers that form a rectangle or square. For example, 1, 3, 8 and 10. Multiply the numbers on opposite corners of the rectangle or square and find their difference. In this example the products are 1 × 10 = 10 and 3 × 8 = 24. The difference is 14. Is it always 14? Try for other rectangles or squares to find out.

1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

Show that a 'tight calendar square' always has a product difference of 7

Start with two adjacent numbers and the two numbers below them to form a square. Let n represent the top left hand number in the pattern. The four numbers are n, n + 1, n + 7 and n + 8 and the products are n(n + 8) and (n + 1)(n + 7).

The difference of the products is

(n + 1)(n + 7) – n(n + 8) = n² + 7n + n + 7 – n²– 8n = 7

So we have proved that when we have a square of two adjacent numbers with the two numbers below them, the difference of products is always 7.

Show that a larger calendar square or rectangle always has a product difference of a multiple of 7

Students can choose a square or rectangle of a given size (say a 2 × 1 rectangle such as that with corners at 1, 3, 8 and 10). The four numbers are then n, n + 2, n + 7 and n + 9. Calculate the product as before, finding and proving a result for calendar rectangles of that shape.

The general case for any calendar rectangle
(This algebra is more appropriate for students working towards level 6)

Ask students to form a conjecture about this difference for any rectangle (includes squares).

Consider ‘vertical’ difference (v) and ‘horizontal’ difference (h). Let n represent the top left number in the rectangle. The other numbers are (n + h), (n + v ) and (n + v + h). Check this numerically with several examples. A good discussion point is that v must be a multiple of 7.

The products will be (n + h)(n + v) and n(n + v + h).

Form the difference of the products:

(n + h)(n + v) – n(n + v + h )

= n² + nv + nh + vh – n² – nh – nv

= vh

This should be consistent with the conjecture, and forms the formal proof of it.

Activity 6: Generalising with algebra

Have students complete the following patterns. Then they work towards a proof of the suggested algebraic statement. Discuss any different forms for the algebraic statement, in particular the differences that arise from alternative labelling.

Pattern 1

Pattern 2

1 + 0 + 12 = 13

2 + 3 + 18 =

3 + 6 + 24 =

4 + 9 + 24 =

10 × 1 + 8 = 18

10 × 2 + 7 =

10 × 3 + 6 =

10 × 4 + 5 =

Algebra statement (ask students to attempt)

n + 3(n – 1) + 6(n + 1) = 10n + 3

Algebra statement (ask students to attempt)

10n + (9 – n) = 9(n + 1)

Proof: (ask students to attempt)

n + 3(n – 1) + 6(n + 1)

= n + 3n – 3 + 6n + 6

= 10n + 3