Properties of Operations: Spin, Shuffle and Split: 2.75

• Indicator of Progress
• Teaching Strategies

Supporting materials

• Related Progression Points
• Developmental Overview of Structure (PDF - 35Kb)
• Developmental Overview of Methods of Calculation (PDF - 38Kb)

Indicator of Progress

Success depends on students being able to use the commutative, associative and distributive properties to help them carry out computation, particularly mentally.

Students use their knowledge of basic number facts and the properties of operations to make strategic decisions to assist in calculation. They know that for addition calculations and for multiplication calculations, the order in which numbers are combined does not matter, but that for subtraction and division it does. The end result is that they use number properties quite automatically, as they shuffle numbers around, split them in convenient ways and combine them in ways that make calculation easier.

Prior to this level, students should be able to use the commutative and associative properties for addition and the commutative property for multiplication, but not the distributive property.

Extensive background information and explanation about the properties of operations.

 

Illustration 1: The distributive property assists calculations

We can calculate 8 × 41 by splitting 41 in a convenient way as 40 + 1. Then we work out 8 × 40 and 8 × 1, to get 320 and 8 respectively, and then add the results to get 328.

Similarly, to work out the price of 4 iTunes which cost $1.95 each, we can work out 4 × $2 (which is $8) and then subtract 4 × 5 cents (which is 20 cents), to get the answer of $7.80.

 

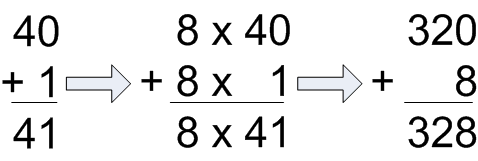
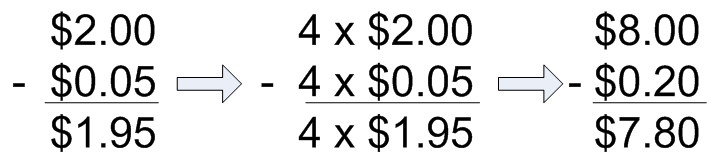
Illustration 2: Commutativity makes learning basic number facts easier

Learning the basic facts for multiplication is easier when students know that the commuted number fact (the spin around) already gives the required answer. This is commutativity. For example, if we know 2 × 7 = 14, we also know that 7 × 2 = 14. This is also true for addition; if we know 6 + 1 = 7, then we know 1 + 6 = 7.

When we begin to learn the 7 times table, for example, part is already known because we already know at least 2 × 7, by knowing 7 × 2 from the two times table, 5 × 7, by knowing 7 × 5 from the five times table, and 10 × 7, by knowing 7 × 10 from the ten times table.

 

Illustration 3: Commutativity and associativity make mental computation easier

Together, the commutative and associative properties of addition mean that numbers and their components can be added in any order. When asked to add 3 + 25 + 37 the student chooses to add 37 and 3 first (and in that order) to get 40, and then adds the remaining 25 to get 65.

 

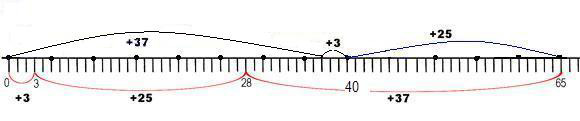
Illustration 4: A common error in the subtraction algorithm

A common error in the written subtraction algorithm is to subtract the numbers the wrong way around. For example, some students will determine that the answer to 74-68 (when written vertically) is 14 instead of 6. This occurs when they can't subtract the bottom digit in the ones column (8) from the top digit (4) so then they subtract the top digit (4) from the bottom (8) instead. This suggests that the child has some uncertainty about whether or not the order matters for subtraction.

Order does not matter for addition, but it does matter for subtraction. Subtraction is not commutative.

Illustration 5

Examples of the types of tasks that would be illustrative of using properties of numbers to solve problems, aligned from the Mathematics Online Interview:

• Question 21 - Mental addition and subtraction using basic strategies
• Question 22 - Mental addition and subtraction using derived strategies

Teaching Strategies

The importance of the commutative, associative and distributive properties and the ways in which they are used can be introduced through incidental teaching as children work with number facts and on mental computation.

The formal terms 'commutative', 'associative' and 'distributive' will not be used with young students, but their implications for calculation and the circumstances in which they apply definitely should. Informal language, such as the “order doesn’t matter when we add [or multiply]” can be used. Children can talk about ‘spin around’ (or turn around) to go from 4 + 6 to 6 + 4 (for example), ‘shuffling’ numbers to combine in more convenient ways, and ‘splitting’ in convenient ways to use the distributive property.

Activity 1:Demonstrating and using the distributive property uses concrete materials to demonstrate why the property works. Students should understand why they can calculate in this way, not just learn that they can.
Activity 2: Mental computation example provides some examples that can be used as a basis for helping students to make strategic computational choices.
Activity 3 : Properties that don’t work is intended to help students appreciate which properties apply for which operations.
Activity 4: Distributive property used with subtraction uses an array to show how multiplication can often be easily done by overestimating and adjusting – in other words by using the distributive property with subtraction instead of addition.

McIntosh and Dole have produced an excellent reference for teaching all aspects of mental computation.

 

Activity 1: Demonstrating and using the distributive property

This activity demonstrates what the distributive property is and why it works. Similar approaches can be used to help demonstrate the other properties. More about Properties of Operations shows how this can be done. The main properties to explain are commutativity of addition (working towards Level 2), and of multiplication (working towards Level 3) and the distributive property (discussed here).

Step 1 Once the array model of multiplication is understood (Level 2.75), the distributive property can be demonstrated with materials as shown in the diagram below. The 5 rows of 10 can be January 05, 2019