Calculations Involving Rates: 5.5

Indicator of Progress
Teaching Strategies

Supporting Materials

Indicator of Progress

Students can use rates to solve problems including those that:

require multi-step calculations
use more than one rate together and
require change of units.

Students should already be familiar with one-step rate calculations and with a variety of rates such as km/hr, m/sec, cents per litre, litres per minute, millilitres per litre, grams per litre. When fractional calculations are required, then even one-step calculations are more difficult.

This is very important because rates occur often in practical calculations.

Illustration 1: Multi-step calculations

Students can perform multi-step calculations when they can answer questions like:

Chlorpromazine injection comes in ampoules that hold 50mg of the drug in 2mL of solution. The dose for children is 0.5mg for each kg of body weight. How much solution must be drawn up into a syringe for a child who weighs 25kg?

Calculations like this are essential in prescribing and administering medication, and the consequences of mistakes can be fatal. There are two January 05, 20194">Illustration 2: Ratios and Rates

The mathematics used with rate questions is very similar to that for ratio questions, since both involve proportional reasoning. The factors that affect the difficulty of ratio problems, such as the type of numbers involved, also impact on the level of difficulty of rate problems.

For more information Easy and hard ratio and proportion questions (Level 5.5)

An additional challenge in rate problems is the necessity to convert between units. For example, consider this problem:

You are driving on a road at a consistent speed of 60 km/hr. A sign says that it is 25 km to your destination. How many minutes will it take to get there?

In this case, as well as dealing with the rate aspects, it is necessary to convert the time units from hours to minutes.

Teaching Strategies

The teaching and learning strategies are based around using a visual aid to organise solution processes, and some puzzles to build intuition about how rates behave.

Activity 1: Direct rate calculations has a selection of direct rate calculations. These are straightforward questions, but the type of numbers involved will affect difficulty, even when students use a calculator.
Activity 2: Multi-step rate calculations has a selection of multi-step rate calculations. Several rates might be used in one question.
Activity 3: The dual number line shows how to use the dual number line as a visual prompt to understand rate problems and organise the solution.
Activity 4: Counter-intuitive rate problems gives two puzzling problems about rates, which sometimes work counter-intuitively.
Activity 5: Drug prescription and administration gives some information about drug administration, a very important application of rates.

Activity 1: Direct rate calculations

The simpler form of direct rate calculations involve easy numbers, where the decision to divide or multiply is reasonably intuitive. For example:

A sprinter runs 100 m in 11 secs. How fast is that in metres per second?
The recommended rate for liquid fertiliser is 50 mL per Litre. How much fertiliser would you use in an 18 L bucket?

Other direct rate calculations are made more difficult by the numbers involved, including fractions or where a change of units is required. For example:

A car is travelling at 90 km/hr. How far will it travel in 27 minutes?
Water flows at a rate of 20L per minute. How long will it take you to fill a glass that holds 375 ml?
Water flows at a rate of 0.20kL per minute. How long will it take you to fill a pond that holds 3.75 kL?

Activity 2: Multi-step rate calculations

The instructions on my packet of soluble orchid food says that the orchid food is to be mixed in water at the rate of 10g for 4L, and that the spoon supplied in the packet holds 5g. How many spoonfuls do I put in my 9L watering can?

Although the numbers are simple in this real world problem, several calculation steps are required, and it is easy to lose track. Why doesn't the packet just say to mix the food at the rate of 5g (one spoonful) for 2L?

You know that your car's average fuel consumption is 9 L per 100 km. If petrol costs 115.5 cents/L, how much will it cost you to do a trip of 550 km?

Both steps in this problem use difficult numbers and so asking students to write out the steps can be helpful even if a calculator is being used.

Activity 3: The dual number line

The dual number line is explained in full detail for ratio problems. However, it is also applicable to rate problems. Here is a simple example.

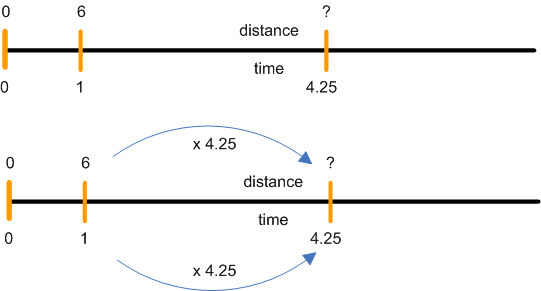
Sally averages 6 km/hr on a fun run. How far can she travel in 4 hours 15 minutes?

One side of the dual number line is for each quantity. The introductory diagram below shows how the times and the distances she can travel are related by the rate. From early years, students can draw dual number lines such as this, to demonstrate their understanding of rates. The formula average speed = distance travelled divided by time taken is a restatement of this table.

Dual number line: plotting distance and time

To solve the problem, the dual number line needs only to be marked with the zero points, the rate (in this case 6 and 1) and the target (in this case 4.25 hours converted from 4 hours 15 minutes). Multiplication by 4.25 moves from 1 to 4.25, so multiplication by 4.25 moves from 6 to the distance required (25.5 km). A dual number line need not be drawn to scale, but if it is, then it helps with estimation.

Dual number line: Time of 4.25 = ? Distance

Activity 4: Counter-intuitive rate problems

It is important that students develop some intuition about how rates behave, and considering some problems where the answers are unexpected can help build this intuition.

Problem 1

A car travels up a hill at 40 km/hr. It travels back down the hill at 60 km/hr. What is the average speed?

Care needs to be taken with problems like these since the 'obvious' solution of 50 km/hr is not correct. The steps should be calculated formally. An average speed of 50 km/hr would occur if the car travelled for the same time at 40 and at 60, but in this problem it travels for the same distance at 40 and at 60 and the average speed works out to be 48 km/hr. An algebraic solution, which shows that the average speed does not depend on the length of the hill climb, is given below. Students without sufficient algebra could solve this problem more easily by selecting an appropriate distance for the travel (e.g. 2 km) and working numerically.

Solution

Let the distance up the hill be d km.
The time to travel up the hill is d /40 hours.
The time to travel down the hill is d /60 hours.
The average speed for the whole trip is total distance (2d ) divided by total time.

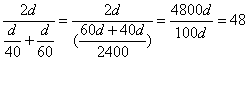
Average speed = 48 km/hr

Problem 2

Vedrin and Vlasta can run at the same speed as each other, and also walk at the same speed. They decide to have a race over 10 km. Vedrin agrees to run for exactly half of the distance. Vlasta agrees to run for exactly half the time it takes her for the whole journey. Who wins?

Solution

It looks like this problem does not have enough information, but it does. The winner is the one who runs the furthest. They start off together, and run the first half of the distance. At the halfway point, Vedrin must stop running and begin to walk. Because this will take longer than the first half, half the time is not yet up, so Vlasta can keep running. This puts Vlasta ahead, and she keeps this lead to the end.

Activity 5: Drug Prescription and Administration

Chlorpromazine injection comes in vials that hold 50mg of the drug in 2mL of solution. The dose for children is 0.5mg for each kg of body weight. How much solution must be drawn up into a syringe for a child who weighs 25kg?

This is a common type of problem in the prescription and administration of drugs. There are two January 05, 2019

Mathematics Developmental Continuum P-10