Ratio and Proportion Questions: 5.5
Supporting materials
- Related Progression Points
- Developmental Overview of Proportional Reasoning and Multiplicative Thinking (PDF - 41Kb)
Indicator of Progress
Ratio and proportion problems can be solved in many different ways. When the ratios are simple (e.g. whole numbers and halves), many students use intuitive methods (e.g. adding or halving) which they cannot generalise to other ratios. This generalisation step is the indicator of progress at progression point 5.5. Success depends on this generalisation step.
A common misconception is to reason additively, instead of multiplicatively (i.e. using proportional reasoning).
Click here to find out more about proportional reasoning.
Illustration 1: Piaget's eel question
Piaget, and later Hart (1981), used some questions about feeding eels to investigate stages of proportional reasoning.
Eels E, F, G and H in the zoo are to be fed according to their length.
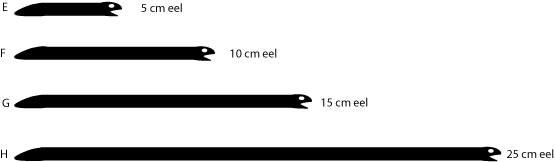
Q1. If E gets 2g of a vitamin mix, how much do F and G get?
Q2. If F gets 12g of fish food, how much does G get?
Q3. If G gets 9 g of frog mash, how much does H get?
Q4. If H gets 10g of shellfish mash, how much does F get?
These questions are of varying difficulties.
- Q1 requires the easiest form of proportional reasoning (doubling and trebling). Students may solve this correctly by repeated addition, but may not see it as multiplication.
- Q2 is only slightly more difficult because adding a half of the amount is a relatively easy step.
- Q3 and Q4 are more difficult because they involve ratios of 3 : 5 etc.
To achieve success at this level students need to work confidently with non-integer ratios such as 2.7 : 8.3.
Illustration 2: Identifying Adders
Additive thinking may be revealed in students' responses to:
Q2. If F gets 12g of fish food, how much does G get?

A common misconception in ratio problems is to use addition or subtraction where multiplication or division is appropriate. Students who answer 17g (instead of the correct 18g) in Q2 are such 'adders'. They see that the grams are 2 more than the length for F (12 = 10 +2), and conclude that the grams are 2 more than the length for G (17 = 15 +2). Alternative, they see that 15 cm is 5 more than 10 cm, and then add this 5 onto the 12 g to get 17 g. They work with a constant difference, when in fact a constant proportion is required.
Teaching Strategies
The teaching strategy here is to begin with diagnostic tasks which will assist teachers to identify which students are only able to operate with simple ratios, and which students have a fuller understanding. The diagnostic tasks will also reveal a group of students with a common misconception, and the activities suggested for them are intended to provoke cognitive conflict, so that their misconception can be exposed to them, and then resolved.
A simple visual device called the dual number line is used to improve students' problem solving. The important thing is to stress that all the relationships are proportional (i.e. multiplicative), not additive. A benefit of the dual number line is that it is applicable in all proportional reasoning problems, so it highlights the commonalities between this topic and others such as percentages.
Activity 1: Using '"Eels" as a diagnostic task and stimulus for class discussion and Activity 2: Diagnostic task and class discussion: Lemon Cordial, Mr Tall and Mr Short are diagnostic tasks which will assist teachers to identify which students are only able to operate with simple ratios, and which students have a fuller understanding.
Activity 3: The dual number lines introduces the dual number line, which is useful for estimating the answer, organising the data and suggesting solutions.
Activity 4: Eliminating adders uses enlargements to address the adders misconception. The activity should use both discussion in groups and as a whole class.
Activity 1: Using "Eels" as a diagnostic task and stimulus for class discussion
Give students a range of short problems to solve with or without calculators. Many students will be able to solve problems with simple ratios - where there is a greater variety of possible methods - than with complicated ratios. The progression in the items will identify those students who need assistance with this work.
The Eels question above provides items of a range of difficulty; add decimals to test fully for greater understanding.
| Approximate Level | |
| Q1 only correct | below 4.0 |
| Q1, Q2 correct | 5.25 |
| Q1, Q2, Q3, Q4 correct | 5.25+ |
| Can also work with decimal ratios | 5.5 |
Two additional questions to reveal full level 5.5 understanding are as follows:
Q5. Two extra eels, Eels J and K, are 12 cm long and 23 cm long respectively. If Eel K is fed 5 g of protein enhancement, how much does Eel J get?
Q6. Two extra eels, Eels L and M, are 13.5 cm long and 21.2 cm long respectively. If Eel M is fed 5.73 g of protein enhancement, how much does Eel L get?
Activity 2: Diagnostic task and class discussion: Lemon Cordial, Mr Tall and Mr Short
On the resource sheet below, Making Lemon Cordial there are five different comparisons to say which lemonade is sweeter. In the first three instances (John & Mary, Dave & Ann, Ed & Rose) whole number ratios are evident. Some students will be able to do these, but will not be able to compare Peter & Elaine, or Howard & Marion. Some students (the 'adders') will stop thinking proportionally and revert to additive approaches in the more difficult problems. Be sure to look at students' reasoning, and not just the answer, which might have been guessed.
Many variations on this task are possible. For example, instead of just asking for the comparison, ask how much sugar or lemon juice the second person needs to make cordial of the same sweetness as the first person. They will demonstrate the same progression of stages; with some students able only to do the later questions.
Question 2 on the resource sheet, Mr Short and Mr Tall, is a medium level difficulty problem from the research of Karplus (1975) and is reported in Hart (1981). Adders will give the incorrect answer 8 (add 2 to 6). More advanced students will add a half, but may not necessarily realise that this is the same as multiplying by 1½.
The problem would be much easier if Mr Tall were 8 matchsticks tall and much harder if he were 7 matchsticks tall. Part of the increased difficulty is due to the complication of working with fractions; another factor is that students may not know that operations like doubling or adding a half are special cases of multiplying by a ratio/scale factor.
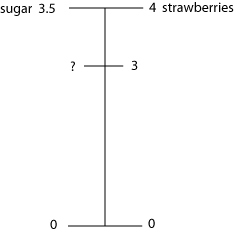
Activity 3: The dual number line
The dual number line is useful in ratio and percentage problems. For ratio problems, one side of the line is marked with quantities of one type and the other with the quantities of the other type.
The dual number line organises the given information and shows which information is missing in each type of problem. If the dual number line is drawn roughly to scale, it is a great help in estimating – always an important first step to any solution.
Dual number lines can also be used to map out solution paths. There are many different ways to solve these problems, so students will not always use the same method as their teachers.
| Tips on teaching with the dual number line: |
| Stress that all the relationships are multiply or divide (not add or subtract). |
| Stress that the same operations are done on both sides. |
| Stress that the directions of the arrows are important. |
| Acknowledge that there are several different correct ways to solve ratio problems. |
Example:
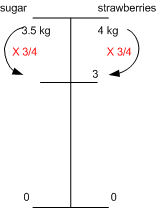
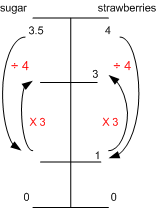
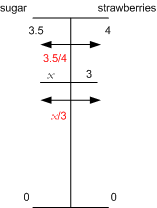
The recipe for strawberry jam says 3.5 kg of sugar for 4 kg of strawberries. I have only 3 kg of strawberries. How much sugar do I need?
There are many possible solutions. This means that students will not always select the same method as their teachers, whether they are using informal or formal methods.
|
Solution 1:
Since three-quarters of the sugar is needed the calculate 3/4 of 3.5, which is 2.625. |
Solution 2:
3.5 ÷ 4 = 0.875 is how much sugar is needed for one kg of strawberries, so 3 × 0.875 = 2.625 is how much is needed for 3kg of strawberries. |
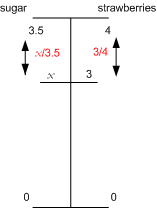
Solution 3:
x/3.5 = 3/4 |
|
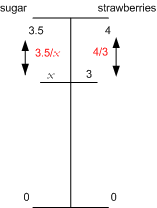
Solution 4:
3.5/x = 4/3 and so |
Solution 5:
4/3.5 = 3/x and then solve for x
|
Solution 6:
x/3 = 3.5/4 |
Activity 4: Eliminating adders
(a) A common wrong approach to proportional reasoning problems is to add or subtract where multiplying or dividing is required. These students are often called 'adders'. For example, in the strawberry problem above, adders will reason as follows:
3.5 kg of sugar needs 4 kg of strawberries. I have one kg less strawberries, so I need 1 kg less sugar.
Answer: 2.5 kg of sugar.
Others will reason as:
3.5 kg of sugar needs 4 kg of strawberries. It requires 0.5 kg less sugar than strawberries, so I need 0.5 kg less sugar for 3 kg strawberries.
Answer: 2.5 kg of sugar.
To highlight that proportional reasoning is required, show situations where additive reasoning makes no sense. First ask students to write down their method in a general way (e.g. I first find the difference in the weights in the recipe (0.5 kg). I always need 0.5 kg less sugar than the strawberries ).
Then ask them to use this rule to find how much sugar for varying quantities of strawberries (e.g. 100 kg strawberries, 0.5 kg strawberries) to see that their own rule does not give sensible answers.
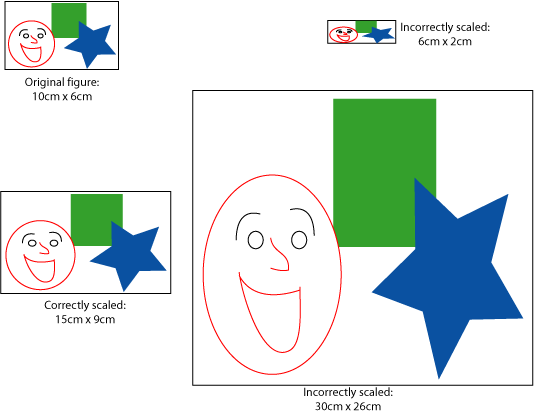
(b) Adders will also use addition or subtraction in making enlargements or reductions. For example, to make a photo of the same shape as a 10cm by 6cm photo, they may subtract 4 cm from the new height to get the new width. Again, get them to make a clear statement of the rule, and then see that it does not work, but makes photos of quite different shapes.
References
Piaget's question, together with a detailed description of students' understanding of ratio, can be found in K.M. Hart (ed.) (1981) Children’s Understanding of Mathematics: 11-15. London: John Murray.
The section on use of the dual number line is adapted from Marston, K. & Stacey, K. (Eds.) (2003). Foundations for Teaching Arithmetic. Version 2. Faculty of Education, University of Melbourne.