Manipulating Symbols: 5.0
Supporting materials
Indicator of Progress
Success depends on students becoming fluent in manipulating symbols. This is essential for using algebra as a language. Success occurs when students can work with expressions involving linear terms, powers and reciprocals. Fluency requires both understanding and practice.
Symbolic manipulation is a well-documented area of difficulty for many students. Although many are able to rearrange numerical equations with understanding, they are unable to manage it when many numbers are replaced by letters.
Fluent symbolic manipulation of more complex expressions is attained at higher levels.
Illustration 1: Manipulating equations
Many students will understand the formula for the perimeter of a rectangle: P = 2L + 2W. The challenge is to produce an equivalent formula for W knowing L and P. Students can think about this in two ways:
(a) They can 'do the same to both sides' of the equation, to make W the subject.
Step 1:
P = 2L + 2W
Step 2: subtract 2L from both sides
P - 2L = 2W
Step 3: divide both sides by 2
W = (P - 2L) / 2
(b) Some students may choose to think of the equation solving as backtracking.
To find P:
Step 1: the unknown number W was doubled,
Step 2: then 2L was added.
So to find W:
Step 1: start with P,
Step 2: subtract 2L, and
Step 3: halve to get W.
Illustration 2: Changing the subject of a formula
Another familiar formula is A = 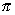 r2.
r2.
To produce a formula for r requires dividing by π and taking the square root of both sides. Alternatively, it can be thought of in backtracking terms. In this context, it is not necessary to deal with the two square roots, although other problems at this level may require it.
Students at this level will appreciate that changing the subject of a formula is the same as solving an equation.
Illustration 3: Algebraic Expectation
Symbolic manipulation needs to improve in accuracy, confidence and speed as students work towards Levels 5 and 6.
Students should be able to quickly, accurately and confidently decide whether:
2 x = x + x OR 2 x = x + 2 OR (x + y) + z = x + y + z OR 2(x + y) + z = 2x + y + z?
Use the prepared algebraic expectation quiz below as it is, or put in your own items.
Teaching Strategies
The general approach suggested is to start with familiar relationships, even more familiar than mensuration formulas, and to use these to establish the equivalences through numerical examples. The mensuration formulas are then used for practice and confirmation.
Practice should follow understanding and cannot replace it. There is definitely a place for skill building not in context, and text books offer many examples of this.
Activity 1: Linking addition and subtraction equations aims to establish understanding of the links between equations such as a = b + c and b = a – c using a formula derived from AFL football scores.
Activity 2: Linking multiplication and division equations aims to establish understanding of links between multiplication and division equations, using a unit cost formula for prices.
Activity 3: Algebraic Expectation Quiz provides a quiz for testing students' accuracy, confidence and speed in algebraic manipulation. The format can be used with your own items.
Activity 1: Linking addition and subtraction equations
1. Use the ‘formula’ that the total number of students is the sum of the number of girls and the number of boys: t = g + b.
How could you find the number of girls if you know the number of boys and the total? Express this as the formula: g = t – b. Similarly b = t – g. The idea here is that the addition is equivalent to two different subtractions.
2. In AFL football the formula for finding the score (in points, p) is p = 6g + b, where g is the number of goals scored and b the number of behinds.
- Confirm that students are familiar with this formula. Many will use it mentally without realising that they are using an algebraic formula! Note that it is still a ‘formula’ even if not expressed in symbols. If needed, help them to express it in symbols and show them how it works.
- Give some total points and goal scores, and ask them to find the number of behinds that were scored. Through questioning, have students explain how they found the answer; this is the required formula, even if expressed in words. Help them express it as a formula.
- Give some total points and behind scores, and ask them to find the number of goals scored. Again help them to express this in words and then in symbols.
3. The examples above will be enough to illustrate the general principle: the addition of two numbers (or terms in a formula) is equivalent to two different subtractions.
Example: 5 = 2 + 3, so 2 = 5 – 3, and also 3 = 5 – 2.
Example: a = b + c, so b = a – c, and also c = a – b.
Example: p = 6g + b, so b = p – 6g and 6g = p – b, and g = (p − b)/6.
The backtracking method may be simpler for many students. They should have previously used backtracking for equation solving with only one unknown. The idea is the same; consider what has been done to the (unknown) letter. For example: p = 6g + b.
To find b we consider the ‘story of b’. We added 6g to get p. So we start from p and subtract 6g . The resulting formula is b = p – 6g.
To find g we note that we multiply by 6, and add b to get p. So we start from p and subtract b, then divide by 6. The resulting formula is g = (p − b) /6.
Note that backtracking can only be applied if the "unknown" occurs only once in the equation.
4. This procedure could be repeated with other alternatives to the football formula, possibly suggested by students. For example, they could examine a formula that describes the amount of change received in terms of the amount of money given to a shopkeeper minus the number of items purchased for a given unit cost. (e.g. how much change if I put $20 into a ticket machine and buy tickets at $3.20 each).
Activity 2: Linking multiplication and division equations
1. When buying a number of the same item we use the unit cost and multiply to find the total price. Price = unit cost × number of items, or p = cn.
Practise using this formula for familiar items.
Now determine how you can find the number of items, given the price and the unit cost; say it in words and write the appropriate formula: n = p/c. Get students to check that it works, every time.
Similarly find the formula for the unit price, given price and number of items: c = p/n.
The idea here is that the multiplication is equivalent to two different divisions.
2. Use the example of the perimeter of a square: P = 4L. How would you find the length of a side, given the perimeter? L = P/4

3. Consider the area of a rectangle: A = LW. Students should use it a few times to recall how it works. How would you find the width if you knew the area and the length?
W = A/L . Students should check that this works every time.
4. Backtracking works here too. Consider the area of a rectangle: A = LW. To find L we realise that we multiply it by W to get A. So we undo these steps: start with A and divide by W, leading to L = A/W.
5. 'Do the same to both sides' works here too. Just divide both sides of the equation by W. If two things are equal, they will still be equal when they are both divided by W.
6. Students can now use one of these methods to rearrange the formula for the area of a triangle: a = bh/2. (Stress that h is vertical height, at right angles to the base).
 |
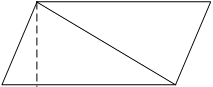
Note that the first step should be multiplying both sides by 2. This leads to the formula
2a = bh. This represents the diagram below. It shows that the triangle is half of a parallelogram for which the formula is a = bh, again where h is the perpendicular height.
 |
Then to find h, we just divide by b. So h = 2a/b . Again students should check that this formula works, every time. Reinforce the general principle.
Activity 3: Algebraic Expectation Quiz
Algebraic expectation is a quality that parallels 'number sense' in the algebra domain. It guides students in all their algebraic work.
The algebraic expectation quiz provides a format for emphasising accuracy, confidence and speed in symbolic manipulation at many levels of learning algebra. It is meant to be fun and also a challenge to students, so it goes fairly fast.
The quiz is administered with a self-timing PowerPoint presentation (PPT - 163Kb). Each student needs a response sheet (Word - 63Kb). Teachers can use the prepared questions or replace them by questions of current focus in the classroom. The set of items in the prepared version is suitable to Level 6. Instructions are given on the first slides.
Some results for beginning Year 11 students from several Victorian high schools are:
- The items asking if 12x/6x = 2 and if 12x/6x = 2x were amongst the most difficult. Most students were confident of their answers, even though they were wrong.
- Only 50% correctly identified that (b+a)2 = a2 +b2 + 2ab. This shows the importance of varying usual patterns.
References
The algebraic expectation quiz has been prepared as part of the RITEMATHS project at the University of Melbourne. http://extranet.edfac.unimelb.edu.au/DSME/RITEMATHS
