Sets: 5.0

• Indicator of Progress
• Teaching Strategies

Supporting materials

• Related Progression Points
• Developmental Overview of Structure (PDF - 35Kb)

Indicator of Progress

Success depends on students being able to use Venn diagrams and tree diagrams to show the relationships of intersection, union, inclusion (subset), and complement between relevant sets. This is related to the correct use of and , or, and not, and the words some, all and none.

Difficulties are likely to be encountered when students have given insufficient thought to the relationships between sets or do not clearly identify the sets involved. The major implications are in the careful use of common but ambiguous words in English.

 

Illustration 1: Set relations and logical thinking

An awareness of relationships between sets is the basis of clear thinking and logic, and frequently misused by media and politicians. To say “Some members of group Z are evil” should not lead to a fear of all members of group Z. The failure in reasoning concerns the fact that the evil-doers are only a (possibly small) subset of group Z. In the diagram, group Z (shaded) is the larger set, with evil-doers in white.

 

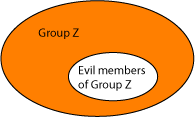
Illustration 2: Contrasting mathematical and everyday meanings of 'and', 'or' and 'not'

Three simple words - 'and', 'or' & 'not' - are the cause of many misunderstandings. In English they can be ambiguous. Their mathematical meanings are precise.

Or

The two possible meanings of the English word ‘or’ confuses many people because of its ambiguity. There is the inclusive or and the exclusive or. 

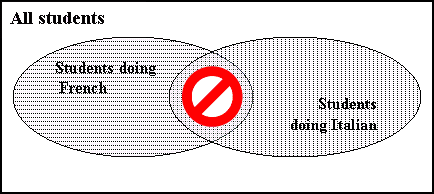
Consider the sentence “At our school, students study French or Italian.” It is not clear in ordinary English whether students are allowed to do both, or whether they have to select just one language.

Inclusive or. This use includes the intersection. The speaker allows the possibility that some students study both French and Italian. Sometimes we feel the need to say ‘A or B or both’ in order to reinforce that the intersection is included, thus forming the ‘union’. In formal mathematics, the word ‘or’ has the inclusive meaning.

 

Exclusive or. Here the intersection is not included. Students do French or do Italian but they may not do both.

And

The two possible meanings of the English word ‘and’ also cause problems due to ambiguity.

What does the set 'males and adults' include?

• only adult males –the intersection of the two sets ‘males’ and ‘adults’, or
• all males and all adults – the union of males and adults, excluding only non-adult females?

This confusion relates to whether the and links the two sets (forming the ‘union’ by including the intersection) or is a requirement that the set being defined has the properties of both sets (forming the ‘intersection’ only).

	Males	Not males (i.e. females)
Adults	Intersection: adult males	Adult females i.e. women
Not adults i.e. children & youth	Male children & male youth	Neither adult nor male i.e. female children & female youth

 

Not

The other key word is ‘not’ and that causes problems too!

What does the set 'not males and adults' include? It is a question of whether not ‘distributes’ across the two sets, like a multiplication

• neither males nor adults i.e. only young females
• females and adults (with the associated ambiguity about ‘and’).

This subject relates closely to careful use of English.

 

Illustration 3: Venn diagrams

Students were asked to make a Venn diagram with the triangles and quadrilaterals below, showing which had right angles.

The student on the left incorrectly put the all the shapes with right angles in the central region. In the central 'intersection' region the student has put triangles and squares, whereas it should contain the shapes which are simultaneously triangles and squares (there are none of these!). The student on the right correctly identified that a third set is involved: the set of shapes with a right angle.

A key skill in this topic is to identify which sets are involved - in this case 3 sets are relevant: the set of triangles, the set of quadrilaterals and the set of shapes with a right-angle.

INCORRECT This student showed the triangles in the red-bordered region, the other quadrilaterals in the green-bordered region and put all the shapes with right angles in the intersection. This meant that some triangles were wrongly in the green (quadrilaterals) region, and some quadrilaterals were wrongly in the red (triangles) region.

CORRECT This student showed the triangles in the red-bordered region, the other quadrilaterals in the green-bordered region and realised that a third region (bordered in yellow) was required for shapes with right angles. There are no shapes in the intersection of the red and green region.

 

Teaching Strategies

The most useful way to address learning in this area is to challenge the students to clarify and justify their thinking through consideration of set relationships. Venn diagrams are often a good way of depicting the relationships. In any case, these activities will be usefully supplemented with group discussions because of the conceptual learning involved (in contrast to developing procedural skills). The topics and concepts involved have a strong relationship to the formation and testing of conjectures, in Working Mathematically.

Activity 1: The set of quadrilaterals aims to illustrate different examples of set relationships by using the set of quadrilaterals as a context. The language use is an important feature.
Activity 2: Power sets aims to further reinforce the set-subset relationship through a study of power sets. It also reinforces the ideas of the empty set and the universal set.
Activity 3: The relationships between categories of numbers aims to demonstrate the possible relationships between sets, by having students examine the relationship between different categories of number: natural (or whole) numbers, integers, rational and real numbers.
Activity 4: Venn diagrams applied to probability presents a Venn diagram in a probability context.

 

Activity 1: The set of quadrilaterals

The set of quadrilaterals provides a nice example of a set with many possible subsets that are related to each other according to their properties (e.g., the set of squares is included in the set of rectangles because squares have all the properties that rectangles have, ie four right angles, and pairs of opposite sides equal in length, together with additional properties, such as having all four sides equal). The set of quadrilaterals can be used to explore ways of describing and representing the relationships between the different subsets (such as trapezia, isosceles trapezia, kites, parallelograms, rhombuses, rectangles, squares). The quadrilaterals resource sheet (Word - 48Kb) defines the shape subsets and suggests a number of activities to help students describe and draw Venn diagrams of the relationships.

 

Activity 2: Power sets

A power set is the set of all the subsets of a set. Power sets are related to choices. For example, consider this situation: “I may give presents to some or all of my three children: A, B and C.” How many children might receive presents?

I might give presents to all of them: ABC. There is 1 way to do that. This is the universal set {A, B, C}

I might give presents to just two of them: AB, AC or BC. There are 3 ways to do that; they are the subsets {A, B}, {A, C}, {B , C}.

I might give presents to only one: A, B or C. There are 3 ways to do that; they are the subsets {A}, {B}, {C}.

Or I might be very miserly and not give a present to anyone. There is just one way to do that, the empty subset {}, which can also be written as Ø.

The pattern 1, 3, 3, 1 has appeared. The total number of ways to give presents to three children is
8 = 2³.

Exploration of this situation with different numbers of children reveals the total number of sets is always a power of 2 (because each element of the set is either in or out) and the number of sets of each size are numbers from Pascal’s triangle.

 

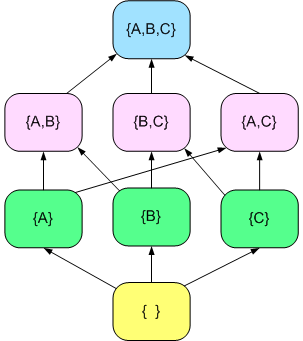This diagram shows the set {A, B, C} and its 3 subsets with two elements, their subsets with one element, and the empty set. The arrows show the 'is a subset of' relation. Not shown on the diagram is the fact that the one element sets are also subsets of {A, B, C} and the empty set is a subset of all of the others. However, this can be deduced by following paths of arrows (e.g. {A} is a subset of {A, B} is a subset of {A, B, C} and so {A} is a subset of {A, B, C}, even though no direct arrow is drawn between {A} and {A, B, C}). This is an example of a partially ordered set: some of the subsets are contained within others (e.g. {A} is a subset of {A, C}), and some are not (e.g. {B} is not a subset of {A, C}). In this example we do not have a tree because there are loops. (Students do not need to know this vocabulary at this stage).

 

Activity 3: The relationships between categories of numbers

Students learn to calculate with different types of number: whole numbers including zero, integers (positive and negative whole numbers and zero), rational numbers (positive and negative fractions) and irrational numbers (including π and most square roots). It is a valuable exercise to consider the relationship between these sets.

This includes a series of subset relationships, in which whole numbers (naturals) are a subset of integers, which are a subset of rationals, which are subsets of reals. Together rationals and irrationals make up the set of ‘real’ numbers. The Venn diagram showing the set of real numbers looks like this.

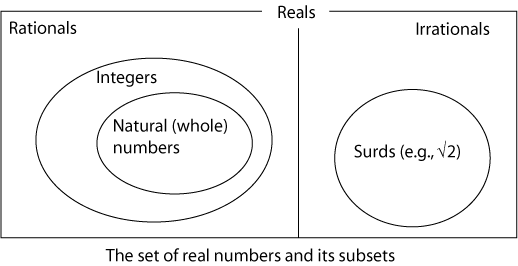
Rational numbers are fractions from integers (e.g. 3/4, 17/ 9, -888/31). Other expressions that use fraction notation (such as √3/2) may not be rationals. Your discussion of this could revise many valuable skills.

• Revise the conversions of fractions to decimals. All fractions convert to decimals, some terminating (those with only powers of 2 or 5 in the denominator) and some repeating (those with primes other than 2 or 5 in the denominator).
• Revise the conversions of terminating decimals to fractions. Note that not all decimals are rational numbers (e.g. √2 is not) but all the terminating and recurring ones are.
• Revise the fact that some fractions reduce to whole numbers (or simpler fractions) by cancelling.
• Revise the process for converting recurring decimals to fractions.
• Demonstrate why √2 is not a rational number.
• Revise that dividing one integer by another will always produce a rational number except, of course, for the critical case of division by 0.
• Revise processes of multiplication and division by fractions and by decimals; look at the issues of placement of decimal points etc.
• Revise the fact that all number laws (associative, commutative, distributive) apply to all real numbers.

 

Activity 4: Venn diagrams applied to probability

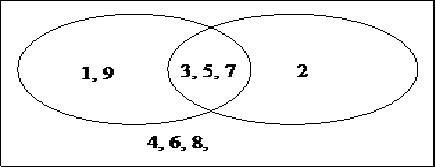
Venn diagrams are especially useful when students learn probability, to help them think clearly about compound events and their probabilities. Consider, for example, a random experiment where students draw a number from 1 to 10 from a hat, and the consequences are determined according to whether the number is odd, or whether the number is prime.

The full set of outcomes is the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. The set of odd numbers is {1, 3, 5, 7, 9}. The set of prime numbers is {2, 3, 5, 7}. The relationships between the sets are depicted in the Venn diagram.

If students get a free notebook if their number is prime and get a snack to eat if their number is odd, then 40% of students are expected to get free notebooks, 50% are expected to get snacks, 30 % are expected to get neither and 30% are expected to get both. These proportions are found by examining which outcomes belong to each Venn diagram region.

This activity relates to chance outcomes above Level 5, so is included here only as an illustration of later uses.