Structure of Equations: 4.5

• Indicator of Progress
• Teaching Strategies

Supporting materials

• Related Progression Points
• Developmental Overview of Structure (PDF - 35Kb)

Indicator of Progress

Success depends on students understanding the structure of algebraic expressions – the combination of letters, numbers and operations that 'tell a story' about a number. This story is constructed using the grammar of the order of operations. This means that brackets, multiplications or divisions and additions or subtractions, all take their proper place to make the story brief and unambiguous.

If they do not appreciate the structure of expressions, whether with numbers or letters, students will have difficulty in all aspects of algebra (solving, substituting, simplifying etc.).

At Level 4.5, the most important structures are linear expressions. At higher levels, students can explain the structure of expressions of increasing complexity.

 

Illustration 1: Understanding an expression through a function machine

Many students are bewildered by the introduction of letters into familiar numerical expressions. For expressions where only one variable is involved in one place it is useful for students to visualise the expression as a ‘story’ of what has been done to transform the unknown number (the variable) into another number. For many students this is helpfully visualised by the function machine, in which the rule is expressed in algebra.

  

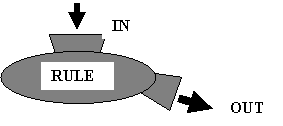
Illustration 2: Explaining and comparing the structure of expressions

Students can explain the algebraic expression 3 (x + 4 ) + 2 as a series of actions on an unknown number such as:

	add 4		multiply by 3		add 2
x		x+4		3(x+4)		3(x+4)+ 2

They can use this to explain how 3 (x + 4 ) + 2 is different to 3 x + 4 + 2

	multiply by 3		add 4		add 2
x		3x		3x+4		3x + 4+2

 

Illustration 3: Substituting and making tables of values

Substituting numerical values into expressions depends on understanding their structure. In the initial stages, a flow-chart can make it easy to work with even complicated expressions.

For example, the expression  can be understood as this series of operations on the unknown number n:

	multiply by 2		subtract 3		divide by 4		add 1
n		2n		2n-3

The flow-charts can be used to guide substituting numbers eg put n = 10 in the above expression:

	multiply by 2		subtract 3		divide by 4		add 1
10		20		17		4.25		5.25

 

Illustration 4: Solving equations by backtracking

Some equations which look complicated are very easy to solve when the structure of the equation is made explicit. One way of doing this is to make the flow-chart that tells the story of what happened to the number.

This equation can be viewed as a series of operations on the value of n, as shown below, leading to the final result of 5.

	multiply by 2		subtract 3		divide by 4		add 1
n								5

Students can mentally 'backtrack' from the known answer, 5, to find the unknown number: subtract 1 (4), multiply by 4 (16) add 3 (19) and halve (9.5). With a little practice students can do this quickly, mentally and correctly every time.

Backtracking is a conceptually simple way of solving some equations.

Teaching Strategies

Familiarity with the structure of expressions, derived from the correct order of operations, is most important in all aspects of algebra. For many students getting this correct in the context of algebra is the critical step to being able to evaluate formulas and to solve equations, either by backtracking or by doing the same operations to both sides.

The general method here is to focus on meaning, expressed clearly with the visual aid of the flow-chart. This should be done frequently, and not just in the introductory weeks. It is far too easy for students to lose track of meaning in the process of manipulations. The flow-charts can also be used for equation solving through backtracking.

Activity 1: From sequences of operations, to flow-charts and equations establishes the link between flow-charts and expressions, by focusing on the meaning of expressions as represented by flow-charts.
Activity 2: From algebraic equations to flow-charts aims to work backwards from an equation to the flow-chart.
Activity 3: Solving equations using flow-charts and backtracking aims to clarify the best use of backtracking, by demonstrating a light touch,and asking for creativity.

Finally, the strengths and limitations of backtracking are discussed.

This set of activities uses flow charts (function machines) to highlight structure. Teachers can also use other approaches eg linking 3(x+2) to the number of objects in three bags each of which originally contained x and had 2 more added. Over time, several approaches may be adopted. The intention here is to do the flow chart approach well.

 

Activity 1: From sequences of operations, to flow-charts and equations

This activity establishes the link between flow-charts and algebraic expressions and equations, by focusing on the meaning of expressions as represented by flow-charts (sets of operations in a particular sequence).

This activity starts with a demonstration and then sets the students free to create their own equations.

1. Start with any number, for example 3, and announce it. Make up a story, a sequence of operations on that number, keeping track of the result at each stage. At the end state the answer.

For example, start with 3, add 5, times 10, subtract 1, makes 79.

Show how to write this as a flow-chart. There is no need for students to set it out formally - simple arrows and diagrams suffice.

	add 5		multiply by 10		subtract 1
3		8		80		79

Then help students write this as an equation, (3 + 5) × 10 – 1 = 79 correctly using the conventions of order of operations. They should check that it is a true number sentence. Substitute several other numbers into the same sequence of operations.

2. Now think of a number, but don’t tell the students. They will have to use the symbol n. Make up another sequence of operations and take them through the same series of steps. At the end, discuss how the solution must follow the conventions of the order of operations, and verify that both representations work.
For example, (n – 4) ÷ 3 + 2 = 6 has the solution n = 16. It has this flow-chart representation:

	subtract 4		divide by 3		add 2
n						6

 

3. Now students create their own stories on a number they have chosen. They write up the flow-chart and equation and let a friend test their versions.

As this takes place, remind students that the order of operations matters and there are different possible correct answers. For example, (n + 3) × 2 = 20 is often written as 2(n + 3) = 20 or using the distributive law, it can also be written as 2n + 6 = 20. However, it cannot be written as 2n + 3 = 20.

(n + 3) × 2 = 20

	add 3		multiply by 2
n				20

SAME

	multiply by 2		add 6
n				20

DIFFERENT

	multiply by 2		add 3
n				20

 

Activity 2: From algebraic equations to flow-charts

This activity starts with equations and asks students to describe it in a flow-chart. Again the order of the operations makes a big difference.

1. Start with very simple equations. Remember that this is not about finding the solutions but expressing the operations as flow-charts and then in words (as many ways as possible), and thinking of real life contexts. Focus on meaning, but make sure they have simple numerical solutions so that the process of testing the equivalence of the equation and the flow-chart is straightforward.
Equations need to have only one occurrence of the variable and it should be near the start of the operations. Suggested equations are:

n + 4 = 10, 2n = 6, n – 5 = 12, 2q + 10 = 18, 2x– 10 = 18 , 2(p+ 1) = 8, 2(m + 1) + 5 = 16,

2. Once you have given students the idea with simple equations, they should make up their own, always making sure that they have simple solutions. This is done by taking the solution and making up the equation using a series of operations, as in Activity 1. They then hand the equation (and its solution) to a friend who creates the flow-chart. They should then discuss the results, including noting any differences and focusing on the meaning to resolve differences between their flow-charts.

 

3. For some simple equations, the flow-charts can be hard to draw. If teachers wish to pursue backtracking in these cases, the techniques will need explicit teaching. In these cases, the operations for undoing need to be carefully considered.

For example, for 20 – 3n = 2, the steps will be:

• start with n,
• then multiply by 3,
• 'subtract from 20',
• giving the result 2.

To solve the equation by backtracking, start with 2, subtract it from 20 (to get 18), divide the 18 by 3 to get 6. The solution is n = 6. Note that the operation to undo 'subtract from 20' is also 'subtract from 20' (not an addition!).

	multiply by 3		subtract from 20
n				2
6		18		2

The next equation has n in the denominator. The flow-chart is: start with n, subtract 1, divide into 24, leaving 8.

Equation		- 1		divide into 24
	n				8

To backtrack, start with 8, divide into 24 (to get 3), add 1, making 4.

Activity 3: Solving equations using flow-charts and backtracking

This activity aims to clarify the best use of backtracking, by demonstrating a light touch, and asking for creativity.

Backtracking works best if it is approached in the spirit of enjoyable mental computation, used in detective mode, working back from a numerical value to the starting number, the solution.

Creating an equation, the flow-chart way

1. Choose any number.

2. Then add, subtract, multiply or divide it by any other number (except 0). At this early stage, avoid negative numbers and fractions.

3. Make a note of what you did, and remember the answer so far.

4. Repeat steps 2 and 3 as often as you like. Now you have created an answer by following a sequence of operations. Write the final answer.

5. Use mental computation to work backwards to work out the number before the last step. Now do the same thing to find the number before that. Continue back to the starting number. This is backtracking. For many people this is done by determining the inverse operation, and using it, mentally.

Writing an equation based on a sequence of operations

• You need to be familiar with the order of operations, brackets, etc.
• Start with n, and write an expression using the first operation on n in the ‘creating’ above.
• Then use the second operation on the result of the first.
• Continue until you have a complex expression showing all the steps. Write it equal to the numerical answer you got above. This is the equation. When you solved the equation by backtracking above, you solved this equation.
• Create more equations by making up a sequence of operations and writing the expressions as you go. Then solve the equation.
• Make up and solve equations for one another, where you don’t tell each other the starting number.

 Backtracking using a calculator

• Repeat the steps above by using a calculator. Now it doesn’t matter if the dividing does not come out exactly, because the calculator will do the work.
• Write the expression as you go, and note the final answer. Write an equation.
• Hand the equation to someone else and challenge them to use a calculator to work backwards.

The appropriate method for backtracking is mental computation, not laborious diagrams and inverse operations. Any tedious drawing of diagrams, writing out of expressions and inverse operations kills the interest and excitement of the new skill. With a little practice, students can do this quickly, mentally and correctly every time.

Backtracking is best done with simple, one line diagrams. A research study showed that students using complicated multi-line diagrams made more errors. See references.

Note: Solving equations by backtracking or 'do the same to both sides'

Backtracking views an equation as a formula, a sequence of unary operations that have taken place on a particular number (the ‘solution’). The left side of an equation is seen as a function rule, and the right side (a single value) is the outcome of the sequence of operations. By undoing these operations in the reverse order, the solution is revealed.

Backtracking is a conceptually simple way of solving some equations. It is conceptually simple because:

• students generally bring to it an intuitive understanding of the 'undoing' idea,
• the flow-chart provides a visual prompt, and
• at every stage after the initial flow-chart is created, students operate on numbers (not algebraic letters) and this is familiar to them,
• it is based on function concepts that students may have already met.

The flow-charting that backtracking is based upon is an important tool for understanding the structure of an algebraic expression, as noted above. This remains a useful tool at all levels of algebra. For example, a flow-chart clarifies the two expressions below.

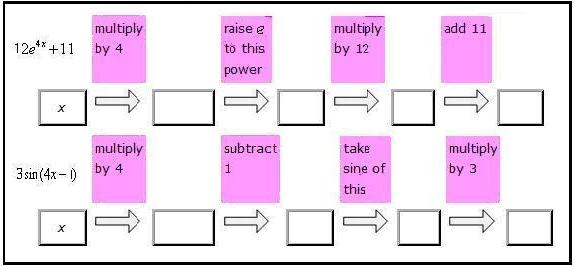
There are also several important limitations of backtracking:

• it only applies to equations with one occurrence of the unknown, so, for example, it could not be used to solve the equation x + 1 = 2x ,
• sometimes, even for simple expressions, the flow-charts are hard to draw (eg for the simple equation ¹²/_(-x) = 3),
• its focus on working with numbers does not assist students in moving to a more algebraic approach.

The method of "do the same to both sides" of an equation is conceptually more difficult, but does not have these limitations.

Teachers should decide when it is worthwhile persisting with backtracking as an equation solving method, when the more powerful 'do the same to both sides' method has been taught.

NOTE: Backtracking works well for quadratic equations, but relies on two important ideas at that stage. They are

• completing the square, ie adding a number to both sides of the equation to make the left side a perfect square;
• when working backwards, find two possible square roots (one positive and one negative).

These two steps are built into the well-known formula.

 

References

MacGregor, M. and Stacey, K. (1995) Backtracking, Brackets, BODMAS and BOMDAS. Australian Mathematics Teacher, 51 (3), pp 28 - 31.