Conceptual Growth for Solving Equations: 5.25
Supporting materials
Indicator of Progress
Success in solving equations requires students to be able to operate with unknowns as well as with numbers, and to be able to operate on equations, not just on expressions or numbers. They need to understand the logic of 'doing the same to both sides' and be able to carry it though efficiently.
Solving equations such as 3(3m − 14) + 22 = 48 + 3m requires students to carry out operations on an equation, for example, to take 3m from both sides. This step also requires students to be able to operate with unknowns (3m), whereas before this, they will have only operated with numbers.
Solving the equation 3(3m − 14) + 22 = 48 is easier because it does not require operating with unknowns in the same way (for example, it can be done by backtracking).
Illustration 1: Operating with unknowns
Quite young students can very often work out an unknown number in a problem like Problem 1.
- Problem 1: I think of a number, double it, add 10 and get the answer 34. What was my number?
However the following two problems are both considerably harder.
- Problem 2: I think of a number, add 10, add my original number and get the answer 34. What was my number?
- Problem 3: I think of a number, add 10, and get twice the original number. What was my number?
In Problem 1, although there is an unknown number involved, all of the operations involved are with numbers: start with 34, take away 10 to get 24 and halve that to get the original number 12.
In Problem 2 and Problem 3, it is necessary to operate with the unknowns - to add them together in Problem 2 or to compare an unknown with its double in Problem 3.
This is one of the conceptual changes students need to make, whilst they are learning to deal with the new notations of algebra.
Illustration 2: Operating on an equation
The equation solving action of 'do the same to both sides' requires students to conceptualise an equation as one mathematical object. Previously, students have not had to work with an equation as a whole, but instead work on numbers or expressions.
The logic is that the equation is transformed to another equation which has the same solutions.
| The equation | 3(3m − 14) + 22 = 48 + 3m |
| has the same solution as | 3(3m − 14) + 22 − 3m = 48 + 3m − 3m |
| 3(3m − 14) + 22 − 3m = 48 |
Teaching Strategies
These conceptual changes will occur gradually as students work with new ideas and new notations. Teachers should provide sufficient experiences of sufficient intensity and quantity for conceptual change to be established.
Activity 1 The logic of 'do both to the same sides' begins with looking at the very simple logic underlying the 'do the same to both sides' principle. There are hidden complexities for students in refocussing their attention onto the equation, rather than its components.
Activity 2 Creating equivalent equations gives students the opportunity to create equivalent equations freely. This familiarises them with the process before the additional cognitive load of trying to reach a particular equation solving goal.
Activity 3 Solving equations efficiently suggests that technology can assist students in developing an efficient approach, by providing supported practice.
Activity 4 Practice with depth is an opportunity for students to practise solving the more challenging types of linear equations.
Activity 1: The logic of 'do the same to both sides'
Equivalent equations, better known as DSBS (‘do the same to both sides’), views the equation as an ‘object’ with a particular solution. The method is based on modifying both sides of the equation (at the same time) so that eventually the simplest equivalent equation of all is revealed: x = ‘number’. This is conceptually more difficult than backtracking. However for those equations that do not fit the ‘backtracking’ requirement, this is the only way forward.
The idea can be introduced with a balance model; indeed anything that emphasises that the two sides of the equation are equal.
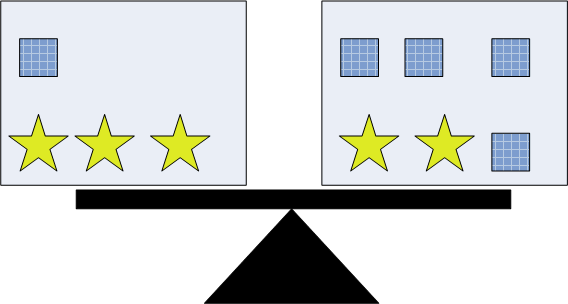
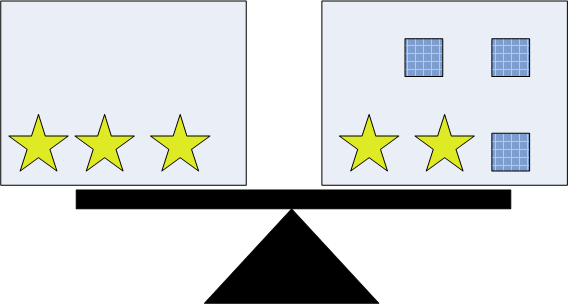
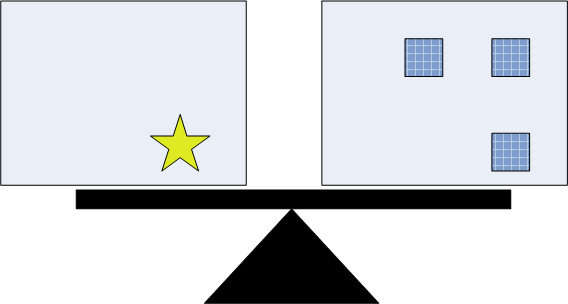
The balance model cannot deal with all cases (e.g. with subtraction). Just use it to introduce the underlying logic. In the balance illustration below,
3a + b = 2a + 4b if and only if 3a = 2a + 3 b if and only if a = 3 b.
|
3a + b = 2a + 4b
|
 |
|
3a = 2a + 3 b
|
 |
|
a = 3 b
|
 |
It is probably best to give examples of these balances numerically (see examples below).
| CORRECT - BALANCED | INCORRECT - UNBALANCED | |
| If the weight of the blue cube was 2 kg and the weight of the yellow star was 6 kg, then the first balance says: | If the weight of the blue cube was 2 kg then the weight of the yellow star cannot be 3 kg. | |
|
(1 × 2) + (3 × 6) = (4 × 2) + (2 × 6) 2 + 18 = 8 + 12 20 = 20 |
1 × (wt blue cube) + 3 × (wt yellow star) = 1×2 + 3×3 = 11 4× (wt blue cube) + 2 × (wt yellow star) = 4×2 + 2×3 = 14 The right hand side of the balance is heavier than the left side - not balanced. |
Activity 2: Creating equivalent equations
Equations that may be changed from one to the other by ‘doing the same to both sides’ are called ‘equivalent equations’. They will have the same solution(s). The usual use of this process is to start with a complex equation and eventually simplify it by creating a series of equivalent equations, until they reach the solution.
Students can understand this process well if they learn to do it in reverse. They can start with the simplest equation of all and complicate it, checking that all the solutions along the way are really equivalent, and have the same solution. Teachers may like to make up the first equations, but then students can make them up themselves.
For example, start with n = 2. This is the simplest solution. The number 2 will be the solution to all the equivalent equations, which are created by doing the same to both sides.
n = 2
| n = 2 | ||
| Multiply both sides by 3 | 3n = 6 | The solution is still n = 2 |
| Add 2n to both side | 5n = 2n + 6 | The solution is still n = 2 |
| Subtract 5 from both sides | 5n – 5 = 2n + 1 | The solution is still n = 2 |
| Factorise left side | 5(n – 1) = 2n + 1 | The solution is still n = 2 |
There is no end to the variety of complications they can make, and to the order in which they can be done. Unless students multiply or divide by 0, the solution will be the same. This should be checked by substitution.
All students can begin with the same equation. The variety of equations can be collected together and checked by other students.
The logic of 'do the same to both sides' should be stressed.
- If two things are equal, then they stay equal if the same operation is carried out on them both.
- If the first equation is true when n = 2, then the other equations will be true when n = 2.
Activity 3: Solving equations efficiently
The process of solving equations by creating equivalent equations is a series of 'do the same to both sides' actions followed by simplifications.
| Start with | initial equation | 3x + 4 = x - 12 |
| do something to both sides | get an equivalent equation | 3x + 4 + 12 = x - 12 + 12 |
| simplify each side | 3x + 16 = x | |
| do something to both sides | get another equivalent equation | 3x + 16 - x = x - x |
| simplify each side | 2x + 16 = 0 | |
| do something to both sides | get another equivalent equation | 2x + 16 -16 = 0 - 16 |
| simplify each side | 2x = -16 | |
| repeat until eventually getting the simplest equation | x = answer | x = -8 |
When students understand this process and why it works they still have to learn to carry it out efficiently, because the basic mantra DSBS (do the same to both sides) provides no guidance about the best order in which to do the operations.
Due to a lack of awareness of the structure of an equation, students can often ‘do the same to both sides’ and find that the equation is getting far more complex, not simpler.
For example, take 3n + 4 = 5(n – 3).
Some students will divide both sides by 3 and get very confused. The best first step is to expand the brackets, to give 3n + 4 = 5n – 15. Should the students then subtract 3n, 5n, 4 (from both sides) or add 15? The consequences of each choice should be explored so that the students understand why some orders of steps are more efficient than others. It turns out that the best order is closely related to the ‘reversed order’ in backtracking.
In classes that have access to CAS (computer algebra systems on calculators or computers), students can very easily experiment with DSBS actions, so that they can develop some intuition about what order is likely to be the most efficient. It is harder to carry out a wide range of actions by hand, because students make too many manipulation errors.
With CAS to demonstrate many examples, students can see:
- that the solutions are preserved by any DSBS action (except multiply by 0), so wrong actions are not fatal
- that some sequences of DSBS actions are much more efficient than others in getting to a solution.
Activity 4: Practice with depth
The Third International Mathematics and Science Study 1996 showed that only 35% of Australian students correctly solved the equation
10x - 15 = 5x + 20.
Part of the difficulty of this equation is the fact that the unknown is on both sides, and so it is not amenable to a backtracking solution.
Examples
A word problem leading to an equation with an unknown on one side
Carmella wishes to sell ceramic bowls. Her initial costs are $250 for the kiln and $60 for the mould and the clay.
How many bowls should she produce to break even, if she sells them for $14 each?
x = number of bowls to break even.
250 + 60 = 14x
A word problem leading to an equation with an unknown on both sides
Cameron wishes to sell ceramic bowls. His initial costs are $250 for the kiln and $60 for the mould and $2 per bowl for the clay.
How many bowls should he produce to break even, if he sells them for $14 each?
x = number of bowls to break even.
250 + 60 + 2x = 14x
