Equivalence: 4.0
Supporting materials
Indicator of Progress
Students can solve simple addition and subtraction number sentences by seeing relationships between numbers in uncalculated form. Click here to read more.
Prior to this, students will tend to carry out all calculations and work step by step to an answer, instead of looking at the structure of the number sentence.
Illustration 1: Relational thinking with addition
Students are asked to find the missing number in the number sentence 26 + 39 = 23 + □.
Some students will use a direct computational approach.
They will carry out the addition 26 + 39 = 65, put 65 = 23 + □, and then find that □ = 42.
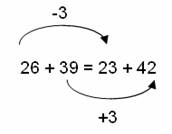
Students who understand that there can be relationships within number expressions will look at the number sentence as a whole and use their knowledge of numbers and operations to find the value of the missing number.
For example, they could use the fact that 26 is 3 more than 23 to say that the missing number must be 3 more than 39 for both sides to be the same.
The latter thinking is a good foundation for algebra, where 'uncalculated' expressions are often encountered and students need to understand how operations such as addition and subtraction work.
Illustration 2: False relational thinking with subtraction
Some students will reason relationally but incorrectly with questions involving differences rather than addition.
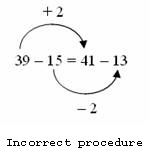
For example, to solve 39 - 15 = □ - 13, some students will apply the same strategy for balancing that worked for addition. In the diagram, the student has reasoned that because 13 is 2 less than 15, the box must be 2 more than 39.
This is a common error. Students who were successful with relational thinking for addition often have difficulties with subtraction.
Teaching Strategies
These activities engage students in examining reasoning, and discussing its validity. They have the opportunity to present their reasoning to other students, helping the group focus on the 'whys' of mathematics, not just the 'whats.'
Activity 1: Keeping the sum the same introduces some 'relational' reasoning and then provides opportunities for students to try it themselves.
Activity 2: Keeping the difference the same extends the reasoning to number sentences where each side is a difference rather than a sum. Many students will overgeneralise the thinking that they applied to addition, and apply it incorrectly to subtraction. This underlines the importance of having each student recreate their own reasoning, not mimic the reasoning of others.
It is easy to create similar activities with number sentences involving multiplication and division, although these will be at a higher achievement level.
Activity 1: Keeping the sum the same
Students are asked to follow another student’s relational reasoning prior to trying to use the same type of reasoning themselves.
Instead of first calculating 7 + 6 and then subtracting 5, Chris uses his understanding of the properties of addition to reason out the answer logically.
The first part is best used as a discussion activity, where students can explain their reasoning to the group for several examples, and make up number sentences themselves for others to consider.
To keep the two sides equal, students need to recognise that if a number on the right side is 1 more than a number on the left side, then the other right hand number must be 1 less than the corresponding left hand number. These ideas are easy to explain diagrammatically.
|
 |
7 purple blocks 6 orange blocks ? white blocks 5 green blocks
|
In the second part of the activity, students work individually to use similar reasoning strategies to solve a set of number sentences on the resource sheet Keeping the sum the same (Word - 31Kb). They should explain their reasoning in a similar way to the reasoning used by Chris. Of course, variations on this reasoning pattern may be possible and interesting to the students.
Students will find the greatest power of their new skill in working out very large missing numbers easily, such as: 278 + 629 = □ + 631
Activity 2: Keeping the difference the same
Activity 2 extends the relational thinking in Activity 1 to number sentences involving differences. Students may be surprised to see that the same strategy of increasing one number to compensate for reducing the other number does not work with differences.
For example, 39 – 15 = □ – 13.
Discuss the following examples of a student's reasoning. Which, if either, is correct? Are the two sides equal? What is wrong with the reasoning?
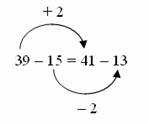 |
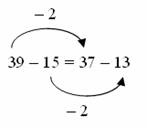 |
The important concept is that the difference must be kept the same on both sides, compared with the previous activity where the sum had to be kept the same on both sides. Because 13 is 2 less than 15, then the missing number must be 2 less than 39 to keep the difference the same.
Discuss some more number sentences involving differences, starting with small numbers where the missing number is more immediately apparent and building up to examples with larger numbers. Examples will have the missing number before and after the subtraction.
| 10 – 7 = □ – 5 | 20 – 8 = □ – 10 | □ – 14 = 46 – 11 | 67 – 15 = □ – 19 |
| □ – 29 = 185 – 23 | 10 – 7 = 12 – □ | 39 – 15 = 41 – □ | 99 – □ = 90 – 59 |
Again students should recognise that the difference must be kept the same.
Students may now be ready to tackle the resource sheet Keeping the difference the same (Word - 33Kb), using the idea that the difference must be kept the same. Again, they will see their new found power to find quick answers to questions with large numbers such as
1000000 - 45678 = 999999 - □.
