Rules for Sequences: 4.0

• Indicator of Progress
• Teaching Strategies
• Further Resources

Supporting materials

• Related Progression Points
• Developmental Overview of Structure (PDF - 35Kb)
• Developmental Overview of Working Mathematically (PDF - 31Kb)

Indicator of Progress

Students will be able to work in two ways with a sequence of numbers. They will know how to use a simple recursion rule to create or extend a number sequence, and be able to describe simple sequences in this way. They will also be able to use a function rule, where each term is defined by operations on its position number. In very simple cases, they will be able to find the function rule for a sequence.

Many students encounter difficulties when trying to conceptualise the formula idea. Recursion, getting to the next number in the pattern by doing something to the previous, is often easier in simple formulas.

Find out more about rules for sequences.

 

Illustration 1: Examples of sequences, recursion rules and function rules

A sequence is a list of numbers, or terms, that goes on indefinitely.

We can say how a sequence continues in two ways:

• using recursion (which describes how a term is produced from the terms or terms before it)
• or by a function rule (which tells how to calculate a term, based on its position).

The sequence of even numbers 2, 4, 6, 8, 10, 12 ... has the recursion rule: 'the next term is 2 more than the one before it '.
This gives us 14 (= 12 + 2), 16 (= 14 + 2), 18 (= 16 + 2) as the next three terms.

This sequence of even numbers also has a function rule, since each term is '2 × its position in the sequence'.
This gives us 1st term is 2 (= 2 × 1) , the 2nd term is 4 (= 2 × 2), the 3rd term is 6 (= 2 × 3), and so on. As 12 is the 6th term, the 7th term will be 14 (= 2 × 7), the  8th term is 16 (= 2 × 8 ), the 9th term is 18 (= 2 ×  9), and the 10th term is 20 (= 2 × 10), and so on.

For more examples of such sequences and further explanation of function rules and recursion rules, click here.

 

Illustration 2: Some examples

At Level 4, students will be able to:

• use the recursion rule 'Start at 2 and repeatedly add 10' to get the sequence 2, 12, 22, 32, 42 ...
• use the formula 'Multiply the position number by 10 and subtract 8' to get the same sequence.
• find the recursion rule for the sequence 100, 98, 96, 94 ... (start at 100 and repeatedly subtract 2).
• find the formula for the sequence 5, 10, 15, 20 ... (just multiply the position number by 5).

At this level, they may not be able to find the formula for the sequence 3, 8, 13, 18, 23, 28 ... although they will be able to find its recursion rule.

 

Illustration 3: Confusions between recursion rules and formulas

Algebra is a language in which formulas can be written, used and studied. Until senior mathematics, students do not write recursion rules algebraically, but they learn to write formulas when working towards Levels 5 and 6.

If they have not clarified the two ideas, of a recursion rule and a formula based on the position number, when asked to write formulas to describe sequences, students working towards Levels 5 and 6 will often confuse the two and try to write the recursion rule instead.

x	1	2	3	4	5	6
y	7	11	15	19	23	27

For example, instead of correctly writing y = 4x + 3 to describe the sequence above (as a formula), they might write shorthand statements such as :

• x + 1 = y + 4 ('when you add 1 to x, you add 4 to y')
• x = 7 + 4y (something like 'start at 7 and keep adding 4 to get y')
• y = y + 4, x = x+1 (add 4 to the previous value of y to get the next one, add 1 to get next value of x)
• x = 3y ('there are three numbers missing between the y ' - i.e. between 7 and 11, the numbers 8, 9 and 10 are missing)

This incorrect algebra stems from confusion between the recursion rule and the formula.

 

Teaching Strategies

The underlying idea is number patterning and the different ways it can be summarised mathematically. The general approach is to use one method to develop a number pattern (or sequence of numbers) and then explore the pattern using other methods. Through discussion, the strengths of each method and the differences in approach can be grasped and generalised.

Activity 1: Recycling numbers develops the concept of recursion by relating it to the everyday concept of recycling, and using calculators and a spreadsheet to develop this idea further.
Activity 2: Even and odd numbers develops a formula for the sequence of even and odd numbers and introduces the ‘function machine’.
Activity 3: Linking recursion rules and formulas develops a link between certain recursion rules and formulas by using simple formulas to produce sequences and noting the recursion rules associated with the formulas.
Activity 4: Familiarity with numbers is the key to finding patterns is a reminder that students' ability to recognise sequences comes from familiarity with number patterns and properties and good mental arithmetic.
Activity 5: Why have both recursion rules and formulas? provides an example where students look for the recursion relation, but miss an important formula. It is also a reminder that students need to know why two ways of describing sequences are important.
Activity 6: Recursion rules in spreadsheets recalls simple uses of recursion in spreadsheets.

 

Activity 1: Recycling numbers

The diagram shows a ‘virtual machine’, a way of thinking about recursion. You put one number into the machine and the recursion rule changes it and shows you the second number in the pattern. However, this number immediately goes back into the machine and is changed by the same recursion rule to the third number, and so on.

  

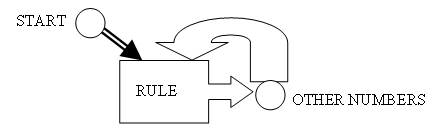
Get students to try one: start with 2 and use the recursion rule ‘add 3 each time’. They should get the pattern 2, 5, 8, 11 etc.

They will see that the same rule and a different starting number gives a different pattern; for example, ‘start with 1 and add 3 each time’ gives 1, 4, 7, 10, 13 etc.

Also the same starting number and a different adding rule gives a different pattern; for example, ‘start with 2 and add 4 each time’ gives 2, 6, 10, 14,18, 22 etc.

It also works with subtracting (but you will need to start with suitably high numbers). For example, ‘start with 30 and subtract 4 each time’ gives 30, 26, 22, 18, 14, 10 etc. The same numbers appear as in the previous sequence, but in reverse order. It is a different pattern, but shows the link between ‘add 4’ and ‘subtract 4’. If you let it run into negative numbers students will see how negative numbers relate.

Other ideas could include:

• ‘Add 7’ is a rule related to the calendar, for example for successive Mondays. The start number will be the date of the first Monday.
• Students can explore doubling, etc.
• Sequences of operations on a calculator can give the same result. For example, on a simple calculator, 2 + 3 = = = = will generate the pattern 2, 5, 8, 11, 14 etc.
• Similar patterns can be explored using rules for subtraction or multiplication.

The spreadsheet ‘Recursion (Excel - 78Kb)’ shows how a simple recursion rule can generate a pattern. The instructions for how to use the spreadsheet are here.

Multi-step recursion rules

There is no need to restrict students to one-step recursion rules. For example, students might make the sequence of numbers to answer the question of how many fish are there in a lake after 10 months if at each month the number of fish doubles, but 10 die?

Start with 20 fish.
End of month 1, we have 2 × 20 - 10 = 30 fish;
End of month 2 we have 2 × 30 - 10 = 50 fish,
End of month 3 we have 2 × 50 - 10 = 90 fish...

Students could discuss the growth of sequences like this, compared to other sequences they deal with.

 

Activity 2: Even and odd numbers

Walk down the street. The odd numbers are on one side, and the even numbers are on the other side.

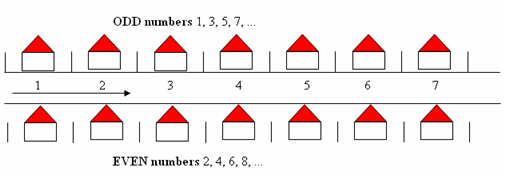
These patterns use the same recursion rule (add 2) but have different starting numbers (2 and 1).

The formula for even numbers:

Here is the table showing the relationship between the number of houses you are along the street and the house number.

Number of houses along the street	1	2	3	4	5	6
Even house numbers	2	4	6	8	10	12

It is easy for students to find the formula for even numbers – the number of houses along the street is just doubled. They can write it in words:

• To get the even house number start with how many houses along you are and double (or multiply by 2).

Even without any mathematical symbols this is still a formula.

The function machine

Just as there is a ‘recycling machine’ for recursion, there is also as ‘function machine’ for formulas. Here it is.

You may put any numbers you like into the top, one at a time (INPUT). The ‘machine’ will produce one number as an OUTPUT, using the formula. If you input the set of numbers 1, 2, 3, 4 ... and use the formula ‘double it’ you will get the set of even numbers, 2, 4, 6, 8 as output.

Ask them to calculate the house number for the 100th house on the even side of the street. Repeat for any other numbers of ‘houses along the street’ that you choose.

Ask them to work out the start number (2) and recursion rule (add 2 each time).

The formula for odd numbers:

Number of houses along the street	1	2	3	4	5	6
Even house numbers	2	4	6	8	10	12
Odd house numbers	1	3	5	7	9	11

Students should be asked to compare the odd numbers with the matching even numbers. This clearly shows that the odd numbers are one less than the evens, so this appears in the formula.

They can write it in words:

• To get the odd house number start with how many houses along you are and double then subtract 1.

Ask them to calculate the house number for the 100th house on the odd side of the street. Repeat for any other numbers of ‘houses along the street’ that you choose.

Ask them to work out the start number (1) and recursion rule (add 2 each time).

 

Activity 3: Linking recursion rules and formulas

In this activity, the recursion rules for a simple type of formula are discovered.

1. Use a simple formula to produce a sequence

Restrict formulas to a combination of multiplying (by any number up to 10) and adding or subtracting (any number up to 10).
Examples: Multiply by 4 then add 3; multiply by 9 then subtract 5. Students should be asked to explore these in different combinations.

Students should complete ‘tables’ to show the results of using the formula.

Position number	1	2	3	4	5	6
Number pattern

2. Find recursion rule for sequence

For each sequence produced by a formula, ask students to find the recursion rule. For example, the formula ‘multiply by 4 then add 3’ produces this pattern.

Position number	1	2	3	4	5	6
Number pattern	7	11	15	19	23	27

The recursion rule is ‘start with 7 and add 4 each time’.

3. Generalise from examples

Before long students will discover that:

• the recursion rule adds, each time, the same number that is being multiplied, and
• the start number for the recursion rule is the sum of the two numbers in the formula.

Example: for the formula ‘multiply by 4 then add 3’ the start number is 7 and we add 4 each time.

The link between ‘multiplying by 4 ’ (in the formula) and ‘adding 4 each time’ (the recursion rule) comes as a wonderful surprise to many students, enabling them to make the link between the two ways of describing a pattern.

4. Link to multiplication tables

The four times table is created by multiplying 'position numbers' by 4 and it also has the property that each number is created by adding 4 to the previous.
The sequence is just the four times table shifted up by 3.

Position number	1	2	3	4	5	6
4 times table	4	8	12	16	20	24
4 times table shifted up by 3	7	11	15	19	23	27
‘multiply by 4 then add 3’	7	11	15	19	23	27

The spreadsheet ‘Formulas and recursion’ (Excel - 78Kb) includes the spreadsheet ‘Recursion’. But it also includes another sheet that uses formulas. It may be used to consolidate the same ideas that are in the two stages above. The instructions on how to use the spreadsheet are here.

 

Activity 4: Familiarity with numbers is the key to finding patterns

The activities above have shown step-by-step ways of finding formulas for a certain type of sequence.

However, students' ability to recognise number patterns in a wide variety of cases comes from their familiarity with numbers, their multiples and factors, differences and other special properties. Good mental arithmetic is essential to see potential links between numbers in a sequence.

Take every opportunity to play with numbers, building up familiarity with them.

For example, the difficulty that many students have in identifying the sequence 1, 4, 9 16, 25, . . . . as square numbers arises from not thinking about numbers as multiples.

Suggestions:

• Spend a couple of minutes each day on a 'Number of the day' with students suggesting many special properties.
• Give students puzzles where they have to guess the next number in a sequence and explain why.
• Look at special classes of numbers (square numbers, cube numbers, perfect numbers, amicable numbers, . . . .)
• Emphasise mental computation.

 

Activity 5: Why have both recursion rules and formulas?

The sequence of square numbers provides a good example of how many students look for a recursion rule rather than a formula.

If they are presented with the sequence: 1, 4, 9, 16, 25, 36 ... many students observe that the numbers are increasing by odd numbers.

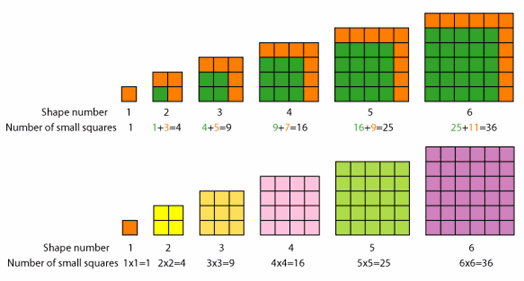
Importantly, however, they do not notice the formula: square the position number.

The recursion formula is easy to use to find some terms of the sequence: for example, after 36 comes (36 + next odd number) = 36 + 13 = 49. However, it relies on us knowing the number we are up to AND what number is the next one we need to add on.

The formula is easy to use to find any term of the sequence, for example, the 1 millionth term is 1 million × 1 million = 1000000000000.

Algebra gives a language for expressing formulas concisely.

Click here (Excel - 35Kb) for a spreadsheet that shows both the increasing odd numbers and the squares.

 

Activity 6: Recursion rules in spreadsheets

The 'fill-down' and 'fill-across' facilities on spreadsheets give a simple way of constructing sequences based on recursion. The sequences can also be readily graphed.

For example,

• entering A1 = 1 and A2 = A1 + 1 and filling down gives the sequence 1, 2, 3, 4, 5 ...
• entering B1 = 4 and B2 = 3*B1 and filling down gives the sequence 4, 12, 36, 108 ...
• entering C1 = 20 and C2 = 2*C1 - 10 gives the sequence 20, 30, 50, 90 ...
• entering D1 = 1 and D2 = 1 and D3 = D1 + D3 and filling down gives the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13 ...

See sample spreadsheet (Excel - 15Kb).

 

Further Resources

The following resource contains section that may be useful when designing learning experiences:

Digilearn object *

Hopper Challenge: ultimate – Students help a frog to jump along a number line. Students estimate the exact finishing point on a number line, after adding or subtracting multiples of tenths or whole numbers to a starting number. For example, 29.5+(12 x 0.2) = 31.9.
(https://www.eduweb.vic.gov.au/dlr/_layouts/dlr/Details.aspx?ID=4877)

* Note that Digilearn is a secure site; DEECD login required.