Partial Products in Multiplication: 4.0

• Indicator of Progress
• Teaching Strategies

Supporting materials

• Related Progression Points
• Developmental Overview of Numbers and Operations (PDF - 2.8Mb)
• Developmental Overview of Methods of Calculation (PDF - 38Kb)

Indicator of Progress

Students can explain the results of multiplication of natural numbers, fractions and decimals using area of a rectangle as a model and identifying the partial products.

Before this, students will have learned to multiply whole numbers, decimals and fractions, but may not have seen that even though the algorithms are different for different types of numbers, the underlying operation of multiplication is the same.

Later, they will explicitly link the partial products and multiplication algorithms to the distributive law.

 

Illustration 1: Inappropriate use of long multiplication algorithm

This student has not appreciated that the additional rows of zeros are redundant. This reveals lack of understanding how the algorithm works.

When we ‘put down the 2 zeros’ to multiply by the 3 in the long multiplication algorithm, we are really multiplying by 300, not just by 3. So this student has worked out 12 × 3 already in the last line. The two rows of zeros are unnecessary.

Students should learn to multiply by 300 mentally in simple cases like this.

 

Illustration 2: Misplacing the decimal point

Some students are only able to explain multiplication of decimal numbers by saying:

“I ignore the decimal point and treat it like whole numbers (27 and 41). After I multiply these I get 1107 and now I need to put back the decimal point, but sometimes I get confused about where it goes. I think I need to line all the points up, so that makes 110.7”

It is hard for this student to remember the rule about where to put the decimal point ‘back’, because she does not routinely estimate the answer as a guide, and she tried to learn the rule without understanding why it worked.

 

Illustration 3: Common error with decimal multiplication

Some students treat decimals as pairs of whole numbers and then apply incorrect reasoning as follows:

“I just multiply the 5 and the 7, so 35, then I multiply the 2 and the 6, so that’s 12.”

This student has overgeneralised a principle applying to addition.

 

Illustration 4: Common error with fraction multiplication

Other students apply incorrect reasoning, as follows

“I just multiply the fractions and then I multiply the 2 and the 3 so I put down the 6.”

This student has overgeneralised a principle applying to addition.

 

 

Teaching Strategies

Students need to regularly revise calculation methods and this revision needs to include revisiting the reasons behind algorithms, not just the rules to follow. If students have a good understanding of why, then they will find rules easier to remember.

To do this, the activities below utilise a visual model (the area of rectangles) to represent multiplication of whole numbers, decimals and fractions. Using the same model for various types of numbers consolidates this representation for students, and emphasises that although the algorithms are different, the underlying multiplication process is the same. The visual model also assists with estimations (upper and lower bounds) to check that answers are within an expected range, which helps to reject wrong answers.

The ideas in this section are related to the distributive property of multiplication over addition. This is not stated as a rule but arises naturally from the model.

For more information see: More About Properties of Operations. (Level 2.75) which addresses the Commutative, associative and distributive properties.

Activity 1: Multiplication of whole numbers showing partial products models multiplication by the area of rectangles, showing the partial products, which are then linked to the ‘long multiplication’ algorithm.
Activity 2: Multiplication of whole numbers using lattice multiplication illustrates an alternative algorithm for multiplication that provides an organised method of recording the partial products.
Activity 3: Multiplication of decimals using partial products extends the array model (or rectangular region) to decimals for three purposes: to show the incorrect reasoning behind a common error, to provide a useful estimation strategy and to provide an alternative calculation strategy.
Activity 4: Multiplication of fractions using partial products again illustrates the usefulness of the rectangular region for illustrating multiplication for three purposes: to show the incorrect reasoning behind a common error, to provide a useful estimation strategy and to provide an alternative calculation strategy.
Activity 5: The National Library of Virtual Manipulatives, provides an excellent resource of animations for supporting learning.

 

Activity 1: Multiplication of whole numbers showing partial products

This activity represents the multiplication of two whole numbers using areas of rectangles, which is an extension of using arrays. Drawing on grid paper with divisions into ten is useful. See: grid (PDF - 84Kb).

Consider the multiplication 54 × 23. The answer is represented by the area of a rectangle with sides 54 and 23.

In this case the area of each small square is 1 and the area of the large squares of the grid is 100.

The sides of the rectangle are divided into intervals based on place value (e.g. 23= 20 + 3 and 54 = 50 + 4).

This gives 4 regions, which are coloured in the diagram.

The products within each of the resulting regions are determined separately (they are referred to as partial products) and then added at the last step.

50 × 20 = 1000

50 × 3 = 150

4 × 20 = 80

4 × 3 = 12

54 × 23 = 1000 + 150 + 80 + 12 = 1242

 

 

This method is useful as:

• it has a strong emphasis on place value
• the operation of multiplication is performed first (several times)
• the operation of addition is performed once (at the end)
• it is visual and therefore more likely to be remembered
• it can be used for all number types (whole numbers, decimals and fractions)
• it is later useful in multiplying algebraic terms (t +2)(t+3) = t² + 2t + 3t + 6.

Use the PowerPoint as a teaching resource with students. See Rectangles and Multiplication (PPT - 121Kb).

Then lead a discussion about estimating the results of multiplication. Often we use a single number as an estimate, but we can also find a ‘band’ that ‘sandwiches’ the answer between two numbers, technically called an upper and a lower bound. (Children don’t need to know these names).

Use the drawing of the rectangle to reason that, for example, the actual answer to 54 × 23 must lie somewhere in the band between:

• a lower bound of 1000 (50 × 20) (this means that we know the answer is more than 1000)
• an upper bound of 1800 (60 × 30) (this means we know the answer is less than 1800).

This means that 54 × 23 is somewhere between 1000 and 1800.

Similarly, use the drawing of the rectangle to reason that the actual answer to 75 × 25 must lie between:

• a lower bound of 1400 (70 × 20)
• an upper bound of 2400 (80 × 30).

This means that 75 × 25 is between 1400 and 2400.

The full advantage of this technique is realised when the calculation involves decimals and/or fractions.

 

Activity 2: Multiplication of whole numbers using lattice multiplication

This activity provides students with an alternative multiplication algorithm. It is useful for enrichment and also for remedial work for students who need an alternative method.

Lattice multiplication gives an organised display of the partial products. Read more about lattice multiplication including its history and how it works, examples and a link to an animation here: Lattice multiplication.

183 × 49 = ?

In lattice multiplication, the partial products are laid out inside a lattice. For example, the partial product 3 × 9 = 27 goes in the bottom right square. Adding along the diagonals, starting with the ones diagonal on the right, accounts for place value and so gives the answer to the multiplication. (see the The National Library of Virtual Manipulatives for a visual representation of lattice multiplication).

 

Use the PowerPoint as a teaching resource with the students. Discuss how lattice multiplication works and the place value behind the diagram. Then give students a new calculation to do using the lattice method, as well as by their standard method. Compare the two ways of recording that lead to the same answer. See: Lattice multiplication (327 x 28) (PPT - 135Kb).

 

Activity 3: Multiplication of decimals using partial products

This activity utilises the rectangular region and partial products (introduced in Activity 1) to:

• provide students with a way of justifying the answer to a decimal multiplication
• provide students with a powerful estimation strategy (upper and lower bounds)
• offer a calculation strategy that is sometimes a useful alternative
• show the incorrect reasoning behind a common error.

Placing the decimal point is a major difficulty for students. Reasoning from first principles, as with this area model, can give them guidance. See: Overgeneralising causes multiplication errors.

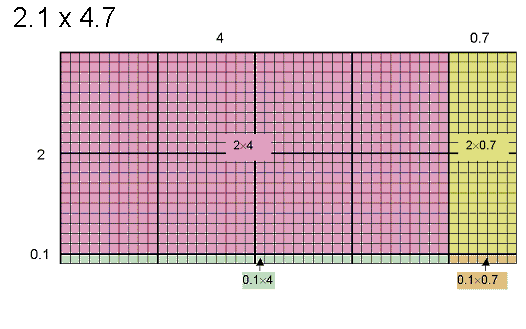
Begin with a sample multiplication, such as 2.1 × 4.7. Model the multiplication as the area of a rectangle with sides 2.1 and 4.7. Draw this rectangle on grid paper as shown below. The grid paper is divided into large squares of area 1 and small squares. There are 100 small squares in a large square, so each of them has an area of 0.01.

From the diagram, we can see that the total area of the rectangle is made of 4 partial products: 2 × 4, 2 × 0.7, 0.1 × 4 and 0.1 × 0.7, which have been coloured differently. Looking at the number of large and small squares we see the areas are:

2 × 4 = 8 (pink)	2 × 0.7 = 1.4 (yellow)	0.1 × 4 = 0.4 (blue)	0.1 × 0.7 = 0.07 (orange)
2.1 × 4.7 = 8 + 1.4 + 0.4 + 0.07 = 9.87

These ideas are presented again in the PowerPoint demonstration which can be used as a teaching resource with the students. This includes suggestions for estimating the results of multiplication involving decimals. As in Activity 1, estimating a ‘band’ that contains the actual answer is useful in rejecting some answers that are wrong because of a misplaced decimal point.

For more information see: More partial products (PPT - 168Kb).

Use the drawing of the rectangle to reason that, for example, the actual answer to 1.5 × 3.6 must lie somewhere in the band between:

• a lower bound of 3 (1 × 3 ) (so 1.5 × 3.6 is greater than 3)
• an upper bound of 8 (2 × 4 ) (so 1.5 × 3.6 is less than 8).

Similarly, use the drawing of the rectangle to reason that the actual answer to 12.75 × 4.63 must lie somewhere in the band between:

• a lower bound of 48 (14 × 4 )
• an upper bound of 65 (13 × 5)

This enables students to check if their answer is reasonable.

 

Activity 4: Multiplication of fractions using partial products

This activity is similar to Activity 3, but based on fractions instead of decimals. It utilises the rectangular region and partial products (introduced in Activity 1) to provide students with a justification for the size of the answer to a multiplication; to provide them with a powerful estimation strategy (upper and lower bounds); and to show the incorrect reasoning behind a common error.

For more information see: Overgeneralising causes multiplication errors.

The diagram below shows that 2 ¹/₃ × 4 ½ can be represented as an area made up of 4 partial products, which are added to give the result of the multiplication.

2 × 4 = 8 (yellow)

2 × 1/2 = 1 (pink)

1/3 × 4 = 4/3 (green)

1/3 × 1/2 = 1/6 (orange)

This gives the same result as the normal algorithm, although it is not as efficient.

Use the PowerPoint as a teaching resource with students. This includes suggestions for estimating the results of multiplication involving fractions. As in Activities 1 and 3, a ‘band’ containing the actual answer is useful in rejecting many wrong answers.

For more information see: More partial products (PPT - 133Kb).

Use the drawing of the rectangle to reason that, for example, the actual answer to 2 ¹/₃ × 4 ¹/₂ must lie in the band between:

• a lower bound of 8 (2 × 4)
• an upper bound of 15 (3 × 5)

 

Activity 5: The National Library of Virtual Manipulatives

The National Library of Virtual Manipulatives - is an excellent resource for animations showing links between models for multiplication and the algorithms, as well as many other mathematical ideas. For example, select ‘Number and Operations’ and then look for:

• Rectangle Multiplication – Visualize the multiplication of two numbers as an area.
• Fractions - Rectangle Multiplication – Visualize and practise multiplying fractions using an area representation.

The images below provide a sample from Rectangle Multiplication. The first image illustrates the link between the area model and the lattice method, and the second image illustrates the link between the area model and the usual long multiplication method.