Addition and Subtraction of Decimals: 3.0

Indicator of Progress
Teaching Strategies

Supporting Materials

Indicator of Progress

At this level students can use efficient written algorithms for the addition and subtraction of decimals to two decimal places.

Success depends on students appreciating that only ‘like things’ can be added or subtracted. Consequently, they need the ability to flexibly rename numbers, as well as recognise when it is important to do so.

Students will already be able to add and subtract money. They will already be able to do a wide range of calculations with decimals using mental calculation, with materials or by informal methods devised by themselves to suit the numbers involved. However, the algorithms give them the power to carry out any addition or subtraction quickly and accurately.

More advanced students will generalise the algorithm for 2 decimal places to any number of decimal places.

Illustration 1: The easiest decimal additions

The addition 1 + 0.4 + 0.03 = 1.43 is very easy for students with a good understanding of place value, but can be very hard for students who meaninglessly follow the algorithm then worry about where to put extra zeros. This should be part of students’ mental repertoire before beginning algorithms. Similarly a subtraction such as 1 – 0.02 is hard by algorithm but easy mentally.

Illustration 2: A Common error in the subtraction algorithm

A common error in the written subtraction algorithm is to subtract the digits the wrong way around. For example, some students will determine that the answer to 72 – 68 (when written vertically) is 16 instead of 4. This occurs when they can’t subtract the bottom digit in the ones column (8) from the top digit (2) so then they subtract the top digit (2) from the bottom (8) instead.

Teachers should encourage students to estimate answers before calculating. It should also be routine that students check their answers to subraction through addition.

Illustration 3: Misplacing the decimal point

Some students are only able to explain addition (or subtraction) of decimal numbers by saying:

“I ignore the decimal point and treat it like whole numbers (316 and 2485). After I add these I get 2801, and now I need to put back the decimal point, but sometimes I get confused about where it goes. If there are two decimal places in the top number and two in the bottom number, then that makes four in the answer, so that would be 0.2801.”

This student has correctly made a link between the algorithm for whole numbers and for decimals, however lacks understanding of the process means that the student is trying to remember rules without reasons, and consequently confuses them.

Teaching Strategies

Teaching algorithms is a long term goal of mathematics teaching. Preliminary understandings include:

good understanding of the meaning of the operation in question
facility with basic facts and
understanding of base ten and place value principles

because our algorithms are designed to work well with our Hindu-Arabic numeration.

Before learning an efficient algorithm, students will have been able to carry out the operation mentally in special cases, and will have devised special methods for dealing with special numbers.

Introducing the formal algorithms will begin with using concrete materials to illustrate their systematic steps (e.g. start at the ones) and recording the actions in an increasingly concise manner.

Practice is essential, but to make it effective students need prompt feedback and revisiting of the underlying principles.

These activities are intended for summary sessions, so that students can get an overview of the processes they are learning. They use a three step cycle to link addition and subtraction algorithms together and to stress the key ideas. However, they could also be used separately for addition and later for subtraction. See: The three step cycle for addition and subtraction.

Activity 1: Revisit addition and subtraction of whole numbers is a revision activity to ensure that students have established the link between actions on materials, as well as the addition and subtraction algorithms for whole numbers. They then replace their focus on the specific numbers with a focus on the steps within the cycles for these algorithms.

Activity 2: Addition and subtraction of decimals follows on from Activity 1. Students use appropriate materials for decimal numbers and then focus on the same cycle of steps within these algorithms.

The three step cycle for addition and subtraction

Addition and subtraction algorithms use a fundamental principle that only ‘like sized pieces’ (e.g. tens) can be added or subtracted. See: About the operations of addition and subtraction.

With concrete materials, this means the first step is to select the pieces of one size (e.g. all the tenths, or all the hundredths). For addition, the pieces of the selected size are then put together. If there are more than ten, then ten are exchanged for 1 larger piece. Then we repeat the process with pieces of another size. Subtraction is similar although ‘in reverse’. The first step is to select the pieces of one size (e.g. all the tenths, or all the hundredths) and ascertain how many have to be taken away. If there are too few, then ten more are obtained by exchanging 1 larger piece. Then we repeat the process with pieces of another size.

These steps are illustrated in the figure below.

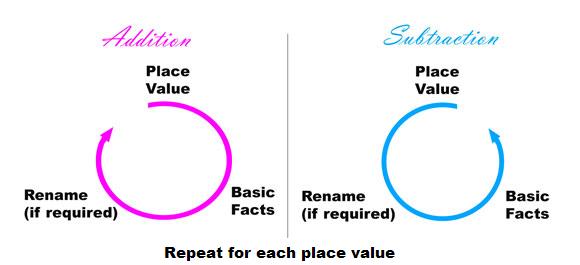
In the symbolic world of the algorithms, the same three step cycles apply, with different terminology.

Addition: consider place value, use basic facts and then rename if required.

Subtraction: consider place value, rename if required, and then use basic facts.

These cycles are indicated in the diagram below (adapted from Booker, 2004).

Three step cycle with symbols

Activity 1: Revisit addition and subtraction of whole numbers

This activity can be adapted to suit students’ individual needs. If your students are already proficient with using materials to model the addition and subtraction of whole numbers, you may choose to reduce or omit Step 1 and move to Steps 2, 3 and 4.

There are two important prerequisites to this. Students should be familiar with representing whole numbers with appropriate materials (such as MAB) and renaming whole numbers.

For more information see:

Number Expanders

Step 1: Focus on the three step cycle with materials

Provide groups of students with appropriate concrete materials (e.g. MAB) and various addition number sentences that they need to demonstrate with the MAB (for example, 235 + 492 = 727).
Now ask the students to demonstrate, with materials, a subtraction number sentence containing the same numbers as their earlier addition (for example 727 − 492 = 235).
Ask students to discuss how the addition and subtraction demonstrations were similar. They should notice that the subtraction is undoing what they did with the addition. (For example, if in the addition, they traded 10 longs for 1 flat, then in the subtraction they will need to do the opposite, i.e. trade 1 flat for 10 longs. This is because addition and subtraction are inverse operations).
Summarise the actions by showing the three step cycle for materials (see above)
Ask students to record their actions, for both the addition and the subtraction situation. Students should be familiar with these written algorithms, and this activity is to consolidate these.

Step 2: Practise the three step cycle with materials

Students practise using the steps in the cycle by demonstrating with materials to other students in the group

Step 3: Present the cycle of steps in the algorithms

Read the PowerPoint presentations beforehand and now present to the students on the board:
- Addition Algorithm for Whole Numbers (PPT - 67Kb)
- Subtraction Algorithm for Whole Numbers (PPT - 59Kb)

Step 4: Practise the cycle of steps without materials

Students need considerable practise using and explaining the steps of both the addition and subtraction algorithms. They should refer to materials when they encounter any difficulty, while recognising that the long-term goal is to use concise written algorithms efficiently.

Activity 2: Addition and subtraction of decimals

This activity follows from Activity 1. Students use appropriate materials for decimal numbers and then focus on using the same cycles of steps within the algorithms. A key idea is to explain the reason for lining up the decimal point as an instance of the fundamental principle that only like sized pieces are added or subtracted.

There are two important prerequisites to this. Students should be familiar with representing decimal numbers with appropriate materials (such as the unit square, redefined MAB) and renaming decimal numbers.

For more information see:

Number Expanders

Step 1: Focus on the actions with the materials

Three step cycle with materials

Provide students with material and various addition number sentences that they need to demonstrate with the materials (for example, 1.35 + 0.92 = 2.27). They should be encouraged to use language carefully (exchanging and renaming).
Now ask the students to demonstrate, with materials, a subtraction number sentence containing the same numbers as their earlier addition, (for example 2.27 − 0.92 = 1.35).
Ask students to discuss how the addition and subtraction demonstrations were similar. This is because addition and subtraction are inverse operations.
Summarise the actions by showing the three step cycle for materials (see above).
Ask students to record their actions, for both the addition and the subtraction situation. Students should be familiar with some written algorithms, and this activity is to consolidate and standardise these.
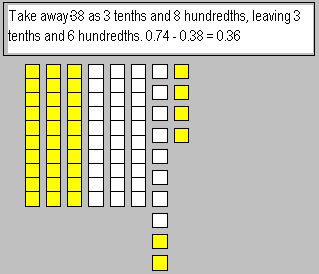
An example of an explanation of subtraction with MAB (using the flat as 1) is as follows.

0.74 – 0.38 = 0.36

1.	2.

3.	4.

Step 2: Practise the cycle of steps with materials

Students swap cards and practise using the steps in the cycle by demonstrating with materials to other students in the group.