Mathematics Developmental Continuum P-10

Deeper Understanding of Pythagoras' Theorem: 5.75

Supporting Materials

 

Back to Top

Indicator of Progress

At this level, students show deeper understanding of Pythagoras’ theorem. They can follow a proof of the theorem, and they can identify applications of Pythagoras’ theorem in complex figures, including three dimensional figures.

At the lower levels of understanding of the theorem, students can use it to calculate a missing side of a right-angled triangle in a simple diagram, first when the missing side is the hypotenuse and then when it is one of the shorter sides. These are straightforward applications, especially when surds are not required.

Deeper understanding of a theorem or property results in:

  • being able to identify its application in complex situations, where the clues to its use are somewhat hidden
  • being able to use it in conjunction with other parts of mathematics (e.g. the algebra of surds) and in multi-step problems
  • being able to follow a proof or give reasons for the truth of the theorem or property.

Illustration 1: Right-angled triangles in 3-D figures

Many students have difficulty visualising all the right-angled triangles in a rectangular prism. This is especially the case when they are only working with 2-D diagrams. To identify this difficulty, ask students to identify all the right angles formed by the edges  (a) inside a rectangular prism (Ans: 3 at each vertex), and then (b) with a rectangular sheet of paper inserted parallel to one end so as to divide the box into 2 halves  and then (c)  with a rectangular sheet of paper inserted diagonally so as to divide the box into 2 halves (the figure below shows half this insert).
To remedy these difficulties with visualisation, provide real models (e.g. a shoebox), and also have students note that they are probably now sitting inside a rectangular prism (their classroom), which they can use as a constantly available model.

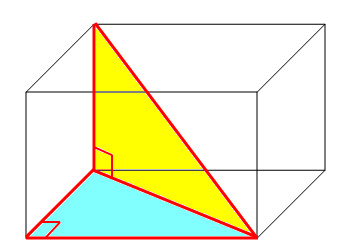
Illustration 2: Right-angled triangles embedded within 2-D figures

Students show increasing mastery of geometric results if they can apply them to cases where the basic geometry is not so evident in the problem.

Examples of hidden applications of Pythagoras’ theorem:

  • knowledge of the angle in a semi-circle is needed to reveal the right-angled triangle in the first diagram
  • knowledge that Pythagoras’ theorem can be applied to three right-angled triangles in the second diagram.
    (See Activity 1)

Illustration 3: Forgetting to square the edge lengths

Students working towards the lower levels may omit some of the steps in calculating the lengths of sides of a triangle even when calculating in simple cases.  For example, student may forget that the edge lengths must be squared before adding, even though they know that they must take the square root of the sum. 

Students without sufficiently strong algebra to reconstruct the transformations for themselves may forget or confuse rote learned rules about to calculate a side length or the hypotenuse.

 

Back to Top

Teaching Strategies

After the basic introduction to Pythagoras’ theorem and practice with straightforward examples finding missing lengths of triangle sides in simple diagrams, students’ understanding will be deepened by:

  • applying the theorem in increasingly complex figures, where the theorem’s application is more deeply hidden
  • working with three-dimensional applications
  • following arguments of why the theorem is true
  • carrying out investigations of related mathematical topics
  • using the theorem in the process of formulating mathematical models.

It is essential to use 3-D models (a shoe box, the classroom) to explain the 3-D version of the theorem.

Activity 1: Hidden 2-D Pythagoras points out two ways in which 2-D diagrams can increase in complexity.
Activity 2: 3-D Pythagoras introduces three-dimensional applications of Pythagoras’ theorem, finding the diagonal of a box theoretically and in three practical situations, checking against measurements.
Activity 3: Pythagorean triples and quadruples investigation has students finding, by pattern search algebra, and internet search, the properties of and formulas to generate these special sets of numbers.
Activity 4: Interactive proofs of Pythagoras’ theorem shows some of the proofs of the theorem that depend on cutting up the squares on the two sides of the triangle and rearranging them to cover the square on the hypotenuse.
Activity 5: A proof of Pythagoras’ theorem presents a short and elegant proof requiring an appropriate amount of algebra for this level.
Activity 6: Rushing to the station requires students to use Pythagoras’ theorem in conjunction with other mathematics, including graphing and numerical tables.
Activity 7: Investigation of shoe lacing patterns is another investigation that enables students to use Pythagoras’ theorem on multiple occasions, using measurements from their own shoes and thinking about the modelling issues.

 

Activity 1 Hidden 2-D Pythagoras

Students show increasing mastery of geometric results if they can apply them to cases where the basic geometry is not so evident in the problem.

Teachers in China call this the ‘principle of variation’ and use it as a framework to plan the teaching of a topic. They begin with the clearest case, then gradually but systematically present examples where the use of the new topic is more and more deeply hidden.

Illustration 2 shows two examples where the right-angled triangles to use in order to find the lengths of all the lines are not obvious. In the circle example, other information (the angle in a semi-circle is a right angle) has to be used to identify the possibility of application of Pythagoras’ theorem.

In the second example, the problem is to find the lengths of the missing sides. Here, there are 3 right-angled triangles, but some students may only see two of them. If 2 right-angled triangles are perceived, the missing lengths can be found. However, if 3 missing right-angled triangles are perceived, all the sides can be found if only two sides (say the 8 and the 6) are given, by just a little algebra.

Teaching that deepens students’ understanding will include examples like these, not just figures of single right-angled triangles.

Activity 2: 3-D Pythagoras

This activity begins with finding the formula for the length of the diagonal of a box, and then suggests 2 real world applications of this idea.

Diagonal formula

3-D problems provide important examples where the right-angled triangles needed to apply Pythagoras’ theorem are difficult for many students to see.

When calculating the length of the diagonal of a rectangular prism, students must recognise two right-angled triangles: the ‘horizontal triangle’ on the base, with sides a, b and x, and the ‘vertical triangle’ with sides x, c and d.
Then it is simple to find the formula for the diagonal length:

   x2 = a2 + b2

   d2 = x2 + c2

So d2 = a2 + b2 + c2

Identifying the right-angled triangles in a drawing of the 3-D box is not easy for many students, so it is important that they work with a 3-dimensional model such as a wire-frame model, or a large open box such as a shoe box and plastic rods. Alternatively, the classroom itself is a box which is always available for visualisation.

How long must the straw be?

This activity is given on the resource sheet ‘How long must the straw be? (PDF - 25Kb)’

The designers of drink cartons must consider the length of straw required so that it will reach the bottom far corner of the carton. If we assume that the straw must protrude by 1.5 cm and that the hole is at one vertex so that the straw can reach into the diagonally opposite corner, the problem is a 3-D Pythagoras’ theorem application, with 1.5 cm added to the calculated long diagonal of the carton. Students can find the required length by measurement inside a drink box, and then devise a method for calculating the length, checking their calculated length with their measured length.

Be sure to discuss the mathematical modelling aspects of this problem with students:

  • is it a good assumption that the straw should reach all the way to the bottom far corner?
  • what difference does it make if the hole is not really at the corner?
  • how can such a long straw be packed on the outside of the box?
  • how many decimal places of accuracy make sense?

Packing a rod in a carton

This activity is also given on the resource sheet  ‘How long must the straw be? (PDF - 25Kb)’

A 2.5 m rod is to be packed diagonally into a rectangular carton for delivery. If the base of the carton is 1.6 m by 1.5 m, what minimum height is required for the carton?
Students should again work with a 3-D model, for example, a shoe box, first measuring, and then calculating.

Discuss aspects of mathematical modelling and the assumptions that have been made, such as:

  • the rod has been assumed to have width 0. What if the rod is wider?
  • would it be better to pack the rod in this carton or get one with length matching the rod?
  • how is the answer different if the rod is packed in a cylinder instead of a box?

Guy ropes for a flagpole

This activity is also presented on the resource sheet ‘How long must the straw be? (PDF - 25Kb)’

A 10 m flagpole is to be supported at the centre of a 12 m square by 5 guy ropes to the north and 5 to the south, at distances 3 m apart. Calculate the required length of each of the guy ropes. A diagram is supplied on the resource sheet.

Activity 3: Pythagorean triples and quadruples investigation

If the lengths of two sides of a right-angled triangle are whole numbers, the third side is not usually a whole number length.  In the special cases where it happens, the set of three whole numbers is called a Pythagorean triple. For example, the whole numbers 5, 12, and 13 can be the lengths of sides of a right-angled triangle because 52 + 122 = 132, so they form a Pythagorean triple {5, 12, 13}. The best known Pythagorean triple is {3, 4, 5}.

A Pythagorean quadruple is a set of four whole numbers that can be the sides and the diagonal of a rectangular prism (box).  Usually if the side lengths are whole numbers, then the diagonal will not be a whole number. The condition for {a, b, c, d} to be a Pythagorean quadruple is that a2 + b2 + c2 = d2 .

One Pythagorean quadruple is {6, 10, 15, 19}.

Some other Pythagorean quadruples are:

62 + 102 + 152
= 36 + 100 + 255
= 361
= 192

{2, 3, 6, 7}
{1, 2, 2, 3}
{3, 4, 12, 13}

To investigate Pythagorean triples and quadruples, students might:

  • find as many as possible, using calculators or spreadsheets
  • look for patterns amongst them, for example
    • every multiple of a triple or quadruple makes another triple or quadruple, so they come in families such as {3, 4, 5}, (6, 8, 10}, {9, 12, 15},
    • no triples are made of 3 odd numbers
  • carry out a library or internet search to find what is known about them.

NRich (http://www.nrich.maths.org/askedNRICH/edited/819.html) gives formulae for calculating sets of Pythagorean quadruples.

Activity 4: Interactive proofs of Pythagoras’ theorem

Many of the proofs of Pythagoras’ theorem involve dissecting squares on the two sides of a right-angled triangle and rearranging the pieces to exactly cover a square drawn on the hypotenuse. Several of these, in interactive form, are available on the internet so students can move pieces to show areas are equal, or change the size of the triangle.

Website 1: A particularly good one is the National Council of Teachers of Mathematics (NCTM) (http://my.nctm.org)

This proof involves shearing transformations of parallelograms and rectangles. It relies on the fact that parallelograms and rectangles with the same base and perpendicular height have the same areas. Shearing does not change their areas.

Website 2: Figure 18 on the website https://www.maa.org/press/periodicals/convergence/proofs-without-words-and-beyond-proofs-without-words-20 has an interactive applet for a common dissection proof, attributed to the 19th century English amateur mathematician, Perigal.

 Drag the dot below the diagram to the right. You will see that the pieces of the two smaller squares can be rearranged to cover the square on the hypotenuse.

Website 3: Another interactive version of Perigal’s proof is available at http://www.cut-the-knot.org/pythagoras/Perigal.shtml. This version allows you to change the dimensions of the right-angled triangle and observe the sizes of the re-arranged dissection, but it does not allow you to drag the pieces. The cut-the-knot website (http://www.cut-the-knot.org/pythagoras/index.shtml) gives 72 proofs of Pythagoras’ theorem.

Students can make a tangram from the dissection used by Perigal. This resource sheet gives a template for Perigal’s proof (PDF - 21Kb). Print it so that students can cut out the pieces from the two small squares to see that the five pieces exactly cover the square on the hypotenuse.

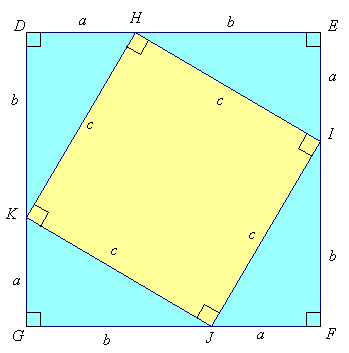
Activity 5: An algebraic proof of Pythagoras’ theorem

Pythagoras’ theorem has been known to humans for about 4000 years, hundreds of years before Pythagoras lived. Pythagoras may have been the first person to find a proof for the theorem. There are many proofs of Pythagoras' theorem.

This diagram can be used for a very simple proof.

The accompanying resource takes students through the steps - An algebraic proof of Pythagoras’ theorem (PDF - 31Kb).

Activity 6: Rushing to the station

Students demonstrate mastery of a topic when they can use it in multi-step problems and in conjunction with other areas of mathematics. The following problem requires several steps to set up the formula for percentage of time saved, and uses algebra and graphing. Some students may also use spreadsheet formulas.

Rushing to the station
On my walk to the station, I can go around two sides of some private land, or I can go across it, which is not really allowed. So I only go across it when I am in a hurry.
The land is 100m wide and 300 m long, so my total walk around the outside is 400m. There is a gate in the opposite fence every 50 m.

What percentage of time do I save by going across instead of around the land? Work it out for coming out at each gate (or for a gate x metres from the first side) and make a table or a graph of the answers.

Now make a table or draw a graph to show how my chance of getting caught (which depends on how long I am on the private land) varies with the time saved.

Make a recommendation to help me decide on my route.

 

Activity 7: Investigation of shoe lacing patterns

Shoes can be laced in several different ways, which require different lengths of shoelaces.

Take measurements from a pair of shoes to make reasonable assumptions about the number of holes and the distances between them. Then calculate the lengths of shoelace required for several different lacing patterns.

Check these mathematical predictions by measurement and account for important differences. In fact, the mathematical model from Pythagoras’ theorem may be quite poor, since it does not account for the amount of shoelace required to change direction, elasticity in laces and different tensions in different parts of the shoe, and the fact that the laced area is not flat.

Students could also investigate what makes an effective and attractive  lacing pattern.  There is a mathematical theory of lacing patterns, but it is not studied at school.

References

Interactive versions of Perigal’s proof:

Back to Top