Counter-Examples: 4.0
Supporting materials
- Related Progression Points
- Developmental Overview of Working Mathematically (PDF - 31Kb)
- Developmental Overview of Numbers and Operations (PDF - 2.8Mb)
Indicator of Progress
Success is achieved when students are able to make a conjecture based on their observations of a number of examples and test the conjecture by making predictions for other instances. They appreciate that finding a counter-example will disprove a mathematical statement, but finding many confirming examples cannot absolutely prove a mathematical statement when it is about an infinite number of cases (e.g. all numbers). If we do not have a logical argument but only rely on examples, we could not be certain that a counter-example will not be found in the future.
Previously, students may think that a few exceptions would not make a mathematical statement false. They might also expect that showing some examples is sufficient to prove that a statement is always true.
As they develop beyond this level, students will become more aware of the need for logical arguments to establish proof and be more able to create these arguments for themselves.
Illustration 1: Differences between mathematical and everyday statements
Some students will not recognise that one counter-example means that a mathematical statement or conjecture is not true. In everyday language they are used to situations where generalisations are made on the basis of something occurring most of the time. I always go to bed at nine o'clock may be a generalisation made, but there may be exceptions. Generalisations are not disproved in everyday life by one counter-example but they are in mathematics. Consideration of a counter-example may result in the refinement of an incorrect generalisation leading to a true generalisation.
Illustration 2: Rows vs rectangles of dots
The Level 4 Standard mentions the conjecture that all numbers can be shown as a rectangular array of dots, which relates to how they can be factorised. There are two ways in which students might attempt to disprove this conjecture, the first valid and the second invalid.
Valid reason
If we think of a number being represented by dots, as shown in the diagram below, then some numbers such as 8 and 9 can be made into rectangles. For example, the diagram shows that 8 dots can each be made into two rectangles (e.g. one is 2 × 4, and the other 4 × 2 ). Nine dots can be made into a 3 × 3 rectangle (which also happens to be a square).
However, 2 dots cannot be arranged as a rectangle, because there can only be one row. Neither can 5 dots. (Note that the Level 4 Standard is not counting a single row of dots as a rectangle). In fact the numbers that cannot be made into a rectangle are 1 and the prime numbers: 2, 3, 5, 7, 11, 13, 17, 19 etc.
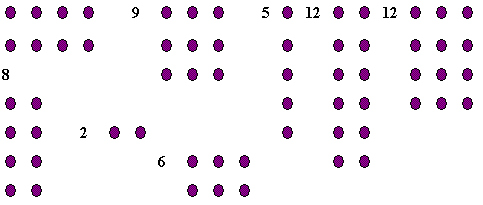 |
Invalid reason
Some students do not wish to recognise squares as examples of rectangles. So numbers like 9, which can only be made as 3 × 3, would also be counter-examples under their definitions. These counter-examples are invalid, as they are based on the wrong meaning of the word 'rectangle'.
Illustration 3: Multiplying makes bigger
The Level 4 Standard mentions the conjecture that ‘multiplication leads to a larger number’. In fact students already know two simple counter-examples to this, but tend to forget them: multiplication by 1 results in no change to the number, and multiplication by 0 results in 0. However it is important that they realise that ‘leads to a larger number’ does not apply to multiplying by a number between zero and one. For example, half of 6 is 3, and ‘half of’ means ‘multiply by one half’.
Knowledge that multiplication (usually) leads to a larger number is a very useful generalisation when learning multiplication tables. However it is dangerous when over-generalised.
For more information: Conceptual obstacles when multiplying and dividing by numbers less than 1 (Level 5.0) which addresses the use of number sense and an understanding of the meaning of operations to estimate the effect of multiplying and dividing by decimals and fractions.
Teaching Strategies
For the Working Mathematically dimension, the main teaching strategies contain three ingredients:
- providing students with real experiences of working mathematically, using open questions that encourage exploration and investigation
- discussing strategies for mathematical investigation including working systematically, making labelled tables, looking for patterns and testing them
- providing opportunities for students to reflect on what they have found and how they have found it, usually through reporting or writing.
The activities below illustrate several points about making conjectures. Conjectures often arise from systematically trying examples and the recording of results in labelled tables. This process can assist in highlighting patterns. Conjectures can be tested by checking predictions against observations/calculations etc. If any counter-examples to a conjecture are found, then the conjecture is disproved, but the original can often be modified to make a better conjecture.
Throughout their learning of mathematics, students will strengthen their appreciation of the nature of arguments that prove that mathematical statements are true.
Activity 1: Which numbers have three factors? highlights the way that conjectures arise from trying examples systematically, and the role of counter-examples. Labelled tables are a powerful tool.
Activity 2: Multiples of 9 uses a well-known ‘fact’ and finds counter-examples and refined conjectures.
Activity 3: Spirolaterals provides wonderful opportunities for conjecturing and testing conjectures in an open investigation.
Activity 4: Arithmagons is another conjecturing activity, where the aim is to find and test a rule for solving a problem.
Activity 5: Goldbach's conjecture presents a famous mathematical conjecture, which is easy to state, and which seems to be true, but for which no-one has yet found a proof. In over 300 years, people have found millions of examples and no counter-example has yet been found.
Activity 1: Which numbers have three factors?
This question can be presented to students as a structured or unstructured investigation. Start with an introductory discussion to help students recall what a factor is. Stress that this investigation is about the number of factors rather than the factors themselves. The number 6, for example, has 4 factors (1, 2, 3, 6) one of which is the number 3.
A good way to begin any problem is to try some examples. A systematic approach using labelled tables is sensible. Putting labels on the tables helps students clarify exactly what they are looking for.
For example, students can make a systematic list of all the factors of numbers, and highlight the ones with 3 factors. Keeping a list of the factors helps students check their work.
| Number | Factors | Number of factors |
|
1
|
1
|
1
|
|
2
|
1, 2
|
2
|
|
3
|
1,3
|
2
|
|
4
|
1, 2, 4
|
3
|
|
5
|
1, 5
|
2
|
|
6
|
1, 2, 3, 6
|
4
|
|
7
|
1, 7
|
2
|
|
8
|
1, 2, 4, 8
|
4
|
|
9
|
1, 3, 9
|
3
|
|
10
|
1, 2, 5, 10
|
4
|
|
11
|
1, 11
|
2
|
|
12
|
1, 2, 3, 4, 6, 12
|
6
|
Looking at this table, students will be able to see that 1 is the only number with just 1 factor (all the others have themselves and 1, and maybe other factors). They will see that the prime numbers have 2 factors. This is what it means to be a prime number.
At this point, students might make some false conjectures. For example, they may observe that 4 is the first number with three factors and 9 is the second and then conjecture that they added 5 to get to 9 and so will add 6 to get the third number with 3 factors ( 9 + 6 = 15). The conjecture has led to a prediction, which can be tested. In this case, the evidence that 15 actually has four factors, not the predicted three, leads them to reject their conjecture. One counter-example is enough.
The investigation will continue as students make conjectures to better fit the accumulating evidence. In fact, the numbers with 3 factors are squares of prime numbers. The factors are 1, the prime number, and the prime number squared eg 1, 2, 4 or 1, 3, 9, or 1, 7, 49.
Reason: Every number has 1 and itself as factors. So a number with three factors can only have one more factor and it must be a repeated factor. This repeated factor cannot itself have factors, or these will make extra factors of the number.
Related investigation
An easier investigation is to ask which numbers have an odd number of factors. The answer is any square number. The reason is that in most numbers the factors come in pairs, but for a square number the square root has to pair with itself.
|
12
|
16
|
23
|
30
|
36
|
|
1 × 12 |
1 × 16
|
1 × 23
|
1 × 30
|
1 × 16
|
|
2 × 6
|
2 × 8
|
1 pair of factors, so 2 factors
|
2 × 15
|
2 × 18
|
|
3 × 4
|
4 × 4
|
3 × 10
|
3 × 12
|
|
|
3 pairs of factors, so 6 factors
|
2 pairs and square root used twice, so 5 factors
|
5 × 6
|
4 × 9
|
|
|
4 pairs of factors, so 8 factors
|
6 × 6
|
|||
|
4 pairs and square root used twice, so 9 factors
|
Activity 2: Refining conjectures: multiples of 9
This investigation begins with an observation that is familiar to students, namely that the digits of numbers in the 9 times tables add to 9. The purpose of this activity is to investigate the truth of this observation, to find its limitations and then to create refined conjectures.
List some of the multiples of 9 on the board: 18, 45, 63, 27, 81, 9 etc. What do these numbers have in common? As well as being multiples of 9, the digits add to 9. This leads to the conjecture that all multiples of 9 have digits that add to 9.
Test it: Does this always happen? Students will discover that the answer is mostly but not always. In the process they will find many other patterns.
Examples that fit the conjecture include 108, 117, 126...207, 216 etc.
Counter-examples include 99, 189, 198, 279, 288, 297 etc. There are many patterns in the counter-examples that lead to new conjectures. Can we change the conjecture to make the counter-examples fit as well? Students may suggest that all multiples of 9 have digits that add to 9 or 18. This does not always work. Lead students to reach the new conjecture that the digits add to a multiple of 9, which is always true.
Partial justification of the conjecture
Spotting patterns like these are useful for learning mathematics,but it is always important to look for general reasons that underlie the patterns. For example, consider a number in the 9 times table. The next number in the table is 9 more. We can add 9 by adding 10 and subtracting one. So the next number in the table is
- one bigger in the tens column
- one less in the ones column.
If we add the new digits together, we get the same answer as adding the earlier digits together.
Example: 63 is a multiple of 9 and 63 = 6 tens + 3 ones.
- Add 9 to 63 by adding ten and subtracting one.
- This gives: 63 + 9 = (6 tens + 3 ones) + (1 ten - 1 one) = 7 tens + 2 ones.
- 7 is 1 more than 6 and 2 is 1 less than 3. 7 + 2 = 6 + 3.
- The sum of digits is the same.
Note that this argument does not apply to the transition from 90 to 99 as the tens stays the same and the ones digit goes up by 9. There will be a similar increase between 180 and 189, going from a sum of 9 to a sum of 18. For consideration, is the sum ever more than 18?
Activity 3: Spirolaterals: conjecturing about shapes and numbers
This is selected as an example of an open-ended investigation with the potential for many conjectures and counter-examples leading to refined conjectures.
How to make a spirolateral
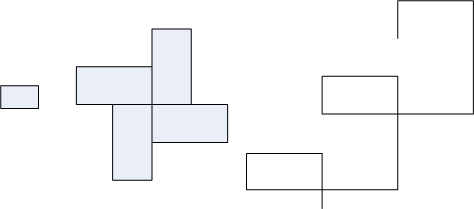
A spirolateral can be made from any list of positive numbers. Take, for example, the sequence of numbers [1, 2, 3]. On a square dot grid, choose a starting dot near the centre. Move 1 space towards the top of the page, turn left, move 2 spaces, turn left, go forward 3 spaces, turn left, go forward 1, turn left, go forward 2, turn left, go forward 3, turn left, go forward 1, and continue indefinitely. This makes a windmill shape, which is called the spirolateral [1, 2, 3] and is shown in the diagram below.
The diagram also shows two other spirolaterals: [1, 2] which is a rectangle and [1, 2, 3, 4] which does not make a closed shape.
|
Three spirolaterals: [1, 2] is a rectangle, [1, 2, 3] is a windmill and [1, 2, 3, 4] never closes.
|
 |
Investigation
There are many questions about spirolaterals to investigate and many conjectures will arise in the process. For example:
- Find other sequences of numbers that make windmill patterns (or rectangles etc).
- Which spirolaterals close and which do not?
- What type of shapes can be made as spirolaterals?
It is best to keep these as open questions. Students should start by trying many examples, building up a portrait gallery of spirolaterals, checking with other students and keeping a record of their conjectures. At every stage, students should try to predict what will happen, (ie make conjectures arising from experience and data), and then test them. If the conjecture appears to be true, they should try to find a convincing reason why it might always be true.
Examples of conjectures:
- Spirolaterals made from sequence of 2 numbers are always just rectangles.
- Spirolaterals made from sequences of 3 numbers are always windmills (nearly always true - what are the exceptions?)
- Spirolaterals made from sequences of 4 numbers never close up (nearly always true - what are the exceptions?)
Activity 4: Arithmagons: Conjecturing about a rule
This activity is here because students often suggest false conjectures as they try to solve it. Testing of predictions shows the need for refining of conjectures.
Some counters are hidden in three containers. The total number of counters in two adjacent containers is written on a line between them. In this puzzle you know the numbers on the lines joining the containers and you need to determine the number of hidden counters in each container.
Here are some examples. In the first diagram, 1 counter has been hidden in each of the two containers at the bottom of the triangle, and 2 have been hidden in the top container. So the numbers written on the lines between the containers are 2 = 1 + 1, 3 = 2 + 1 and 3 = 2 + 1.

Have students set Arithmagon puzzles for each other. For example, I hide 3 counters in one container, 5 in another and 9 in the third. The line numbers are then 8, 12 and 14. My friend's task is to find the numbers 3, 5 and 9 from the line numbers as in the diagram below.

The puzzle is to FIND A RULE for solving arithmagon puzzles. If I give you the numbers on the line, how can you quickly find the hidden numbers of counters? Students will quickly discover that some sets of line numbers cannot be solved using whole numbers. The general problem is to find a method for solving such problems that always works. On the way, many false conjectures will probably appear. Students have to test the method itself, not just check specific cases.
Answer: You can find the total number of hidden counters by adding the three line numbers and dividing by 2. (Why is this?) When you know the total number of hidden counters, you find the number in any one container by subtracting the number in the other two - in other words, subtract the opposite line number. For example, the first arithmagon in the diagram has line numbers 2, 3, 3. The total number of counters hidden is half (3 + 3 + 2) = 4. So there are 4 - 2 in the top container, and 4 - 3 in each of the bottom containers. Students can often discover this rule for themselves.
Activity 5: Goldbach's conjecture
A mathematician named Goldbach is famous for discovering a conjecture which has not yet been proved to be true or false. In the 300 years since the discovery of the conjecture, millions of examples have been found which all support the conjecture being true. No counter-example has been found. But until there is a logical proof that it is true or a counter-example found, mathematicians cannot say whether Goldbach's conjecture is true or false.
Goldbach's conjecture: Every even number, over 2, can be written as a sum of two prime numbers.
For example, 4 = 2 + 2 (2 is prime), 6 = 3 + 3 (3 is prime), 8 = 5 + 3 (5 and 3 are both primes), 10 = 7 + 3...
Students should make a list of prime numbers at least up to 100, and use them to test the truth of the conjecture for even numbers up to 100 or more.
This is included as an example where no-one has yet found a counter-example, but no proof has been found either, so the conjecture remains just that.
