Area of a Circle: 4.75

• Indicator of Progress
• Teaching Strategies

Supporting Materials

• Related Progression Points
• Developmental Overview of Measurement Attributes (PDF - 30Kb)
• Developmental Overview of Working Mathematically (PDF - 31Kb)

 

Indicator of Progress

Success depends on students connecting their knowledge of the formula for the area of a circle, with their knowledge of the areas of rectangles and parallelograms and the length of circumference of a circle.

Being able to use formulas is a lower level of achievement than being able to explain them and connect them to other knowledge. Connected knowledge is a hallmark of good understanding of mathematics and is the beginning of proof.

In this case, being able to find the area of a circle of given radius is at Level 4.75. Being able to give an informal explanation shows higher achievement than this.

 

Levels of understanding of formulas

The levels of understanding of a formula are as follows (illustrated with the area of a circle):

• being able to use the formula in a standard setting (e.g. find area given a radius, find radius given an area)
• being able to use the formula in complex situations (e.g. finding the area of the base of a cone, by identifying the circle and selecting or measuring the appropriate radius)
• being able to adapt the formula (e.g. finding a formula for the area of a sector)
• being able to explain why the formula is correct, moving from informal connections with other known facts to formal proof.

This growth point is connecting the formula for the area of a circle with other known facts.

 

Teaching Strategies

Although students who can explain a formula exhibit a higher achievement than those who can only use it, the teaching paradox is that offering students a justification should always precede practising the use of a formula. Justification comes first in teaching, but students who can provide and explain it, demonstrate a higher achievement.

The formula for the area of a circle cannot be formally proved before students learn calculus. However, Activity 1 provides an informal justification, which shows that the formula for the area of a circle is plausible, based on students' knowledge of:

• area of a parallelogram (or rectangle)
• circumference of a circle, including knowledge of

 

 

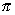
Activity 1: Informal justification for the area of a circle formula

Justification for the area of a circle formula

By dividing a circle into segments and then lining up each segment to form a parallelogram we can see an informal justification for the area formula for a circle. We know that the area of a parallelogram = base × perpendicular height, so using the picture above we can see that if we had taken even smaller segments of the circle and lined them up they would eventually form a parallelogram. The base of the parallelogram is formed by the outer edge of half the segments of the circle which is half the circumference of the circle. The perpendicular height of the parallelogram is the radius. So the area of the 'parallelogram' can be approximated by:  × r2 (reference)

 

The above demonstration can be illustrated by chopping a circle into sectors as shown below.
Cut the circumference into halves, and straighten.
Slot the two parts together.	The more sectors, the more like a rectangle it looks.

At a higher level

Similar reasoning leads to connections between the volume of a sphere and its surface area.
Click here to see how it is done.

 

References

From Marston, K. & Stacey, K. (Eds.) (2003). Foundations for Teaching Arithmetic. Version 2. Faculty of Education, University of Melbourne.