Fairness relates to having an equal chance of winning: 3.0
Supporting materials
Indicator of Progress
Success depends on students understanding that in mathematics, the fairness of a game is associated with players having an equal chance of winning.
This is an early stage in learning about probability. At this stage it is not a quantitative understanding involving calculation. The intention is for students to strengthen their concept of chance and to compare chances, not to measure them.
Illustration 1: Everyday or mathematical meanings of 'fair'
Students may experience difficulty in making the transition from an everyday meaning of fair to the mathematical meaning. The term 'fairness' in everyday life often does not refer to whether or not the game is mathematically fair, but rather, the players' conduct in the game. In mathematics, a game is fair if all players have an equal chance of winning.
A student may believe that a game is 'fair' if all players play according to the rules, rather than thinking about fairness in terms of having an equally likely chance of winning. Students may not associate fairness of a game with the chance of winning. Use of the term 'fair' by children is often associated with whether or not the rules of the game are followed by all players.
For example, if a game involved rolling a die and Player 1 wins if they get 1, 2, 3 or 4 and Player 2 wins if they get a 5 or 6, then many children may consider the game fair as long as the two players roll the die and record their results correctly.
It is important for teachers to be alert to possible confusion for students when everyday and mathematical meanings are different.
Teaching Strategies
Activity 1: Is the game fair? is an awareness
raising activity. Students recognise the need to explore the meaning of the
word 'fair'.
Activity 2: Fair Go! enables
students to explore the phenomenon in an open and creative activity. The focus
here is on whether or not a game is fair by having students play two games:
one that is fair and one that is unfair.
Activity 1: Is the game fair?
Students consider whether the following spinners are fair for a game involving two players. Player 1 wins if the spinner lands on red and Player 2 wins if the spinner lands on blue.
For each spinner, ask students to discuss which player has the best chance of winning (or whether each player has an equal chance of winning) and hence whether or not the game is fair.
In each case there are only two possibilities, red or blue, but they are not always equally likely.
| Spinner 1 |

|
|---|---|
| Spinner 2 |
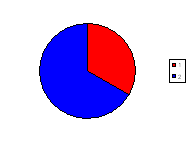
|
| Spinner 3 |
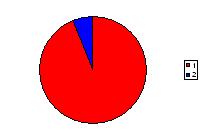
|
Activity 2: Fair Go!
In this activity students explore games for two players. Students discuss whether or not they believe each game is fair and describe the differences in the games. The first two games are unfair, and this will become obvious to the players. They should be able to say, from evidence of playing the games, which player has the greatest chance of winning and that the game is unfair. The third game is mathematically fair. This is harder to observe, and students may be divided about whether it is fair or not.
|
At this level, it is NOT intended that students will calculate any probabilities. Instead, it is intended that by playing the games they will build up an intuitive feel for chance and the likelihood of winning or not. At a higher level, students can calculate the probabilities of winning these games and show whether they are fair or not. |
Game 1: For each roll of the die Player 1 wins if the die shows 5 or 6 and Player 2 is the winner if a 1, 2, 3 or 4 is rolled. First have a discussion about the game and ensure that students understand how it is played and how a player wins. Then get pairs of students to play the game many times, keeping a record of the number of wins for each player. Have a discussion about whether or not students believe the game is fair and who is advantaged.
Game 2: For each game, two dice are rolled. Multiply together the numbers that are rolled. Player 1 wins if the product is odd. Player 2 wins if the product is even. For example, if 3 and 5 are rolled, then player 1 wins because 3 × 5 is 15, an odd number. First have a discussion about the game and ensure that students understand how it is played and how a player wins. Then get pairs of students to play the game many times, keeping a record of the number of wins for each player. Have a discussion about whether or not students believe the game is fair and who is advantaged.
Game 3: For each game, two dice are rolled. Add together the numbers that are rolled. Player 1 wins if the sum is odd. Player 2 wins if the sum is even. For example, if 3 and 5 are rolled, then player 2 wins because 3 + 5 is 8, an even number. First have a discussion about the game and ensure that students understand how it is played and how a player wins. Then get pairs of students to play the game many times, keeping a record of the number of wins for each player. Have a discussion about whether or not students believe the game is fair and who is advantaged.
Once students have played the games, get them to discuss the differences in the games. They should get a sense that the first two games are not fair, but they may be uncertain about Game 3, which is mathematically fair. Lead the students to the understanding that a fair game means that each player has an equal chance of winning.
Provided that enough games are played, students should get a feel that Games 1 and 2 are unfair, and be unsure whether Game 3 is fair or not.
- The first two games are not fair, giving an advantage to player 2 in both cases. If pairs of students from a whole class play these games, then most of the pairs will find that Player 2 wins most of the time in both Games 1 and 2.
- Game 3 is fair. If Game 3 is played by a whole class of pairs of students, some pairs will find that Player 1 wins more games, other pairs will find that Player 2 wins more games. The fact that no one is obviously advantaged is evidence, although not proof, that Game 3 is fair.
These introductory ideas are important for early work on chance. In later years, students will quantify probabilities and consider outcomes for events.
To logically demonstrate that a game is fair or find out how unfair it is, the sample space of all the possible outcomes of the game could be examined to find out which outcomes occur most often, but not at this level.
Further Resources
The following resource contains sections that may be useful when designing learning experiences:
Digilearn object *
Spinners:
explore – students test a coloured spinner (dial with pointer) with three
equal-sized sectors. Students use a tool to build more spinners. Students
choose up to twelve equal-sized sectors. Students choose one of three colours
for each part of a spinner. For example, students make a three-colour spinner
with six red sectors, four yellow sectors and two orange sectors. Students
test the spinner over a number of spins. Students see which colour the pointer
lands on each time. Students watch the graph build after each spin. Students
compare the actual results with the expected results. Students check whether
increasing the proportion of a colour on a spinner increases the chances of
the spinner landing on that colour.
(https://www.eduweb.vic.gov.au/dlr/_layouts/dlr/Details.aspx?ID=4399)
* Note that Digilearn is a secure site; DEECD login required.
