The Meaning of Letters: 4.25
Supporting materials
Indicator of Progress
Students recognise that letters stand for numbers in algebra.
There is a range of common misconceptions related to this indicator of progress. Some students think algebraic letters are abbreviations for words or things and that algebra is a sort of shorthand. Some students think letters stand for units such as metres. Some students think that algebraic letters stand for a secret code. Read more: About the meaning of letters in algebra.
Illustration 1: Algebraic letters do not stand for things
Early experiences with algebra often lead to students developing the misconception that letters stand for objects or abbreviations. For example, f stands for a flower and 5f stands for 5 flowers. In the misguided words of a Year 7 student: “I like algebra because it is all about flowers, animals and things”.
The examples below show teaching that contributes to this common misconception. Rather than use the pronumeral f, which encourages the letter-object/abbreviation interpretation, it would be preferable to use n . This reinforces the concept of pronumeral as number, that is, n is the number of flowers. In this case n = 5. Students should become used to using the word pronumeral instead of ‘letter’, where the word ‘pronumeral’ means ‘for a number’.
‘Fruit salad’ algebra of the type shown below has occurred frequently in textbooks, reinforcing students’ misconception that a letter stands for an object. In this example, a and b are clearly being used as abbreviations for an apple and a banana rather than a pronumeral to represent the number of apples and the number of bananas. It is this type of example that contributes to students’ misunderstanding in algebra.
 |
|
|
If we have two bags, each containing 3 apples and four bananas, how many apples and bananas do we have?
|
|
 |
|
Illustration 2: Diagnostic item
The letter-as-object misconception can recur throughout students' algebra learning. The following diagnostic task from Hart (1981) is useful in levels 4 - 6.
Write an equation which describes the following situation. Use b to stand for the number of blue pencils and r to stand for the number of red pencils.
"I bought some red pencils and some blue pencils and spent a total of 90 cents.
The blue pencils cost 10 cents each and the red pencils cost 6 cents each."
A large survey of students found the following responses were common (Hart, 1981)
(i) 10b + 6r = 90
Correct - 10b is the cost of blue pencils, 6r is the cost of red pencils, together 90 cents
(ii) b + r = 90
Incorrect - "the blue pencils and the red pencils cost 90 cents", letter-as-object misconception)
(iii) b = 6, r = 5 or b = 3, r = 10 or other numerical answer
Incorrect - many students found one solution or more, instead of writing an equation)
(iv) 6b + 5r = 90 or 3b + 10r = 90
Incorrect - "6 blue pencils plus 5 red pencils cost 90 cents", etc. - letter-as-object misconception).
Two of these responses show letter-as-object misconceptions. Response (iv) is especially interesting since these students have worked out how many pencils there might be, and then built this into the equation. For them, using an equation to solve a problem cannot be sensible, since they have to solve it before they can write it.
Illustration 3: Diagnostic Items
Students who had not learned any algebra, and students in the first years of algebra were given these problems. A Victorian study (Stacey & MacGregor, 1997) found that the following responses were common in both of these groups, although more common amongst students who have not learned algebra. These responses reveal algebraic letters interpreted as abbreviations, as well as alphabetic codes etc. The study showed that students' interpretion of algebraic letters according to position in the alphabet is easy to fix, if attention is drawn to it.
| David is 10 cm taller than Con. Con is h cm tall. What can you write for David's height? | |
| Response | Explanation |
| 10 + h, C+10, |
Correct
|
| h10 | Add 10 onto h. |
| Uh, Dh , D | Abbreviated words "Unknown height", David's height , David. |
| 18 or r |
h is the 8th letter of alphabet, therefore 10 more is the 18th letter, r |
| 110 | Think of a reasonable height for Con, add 10 |
| g |
Choose another letter or adjacent letter for David's height. |
| h = h +10, h = +10 | |
| Sue weighs 1 kg less than Chris. Chris weighs y kg. What can you write for Sue's weight? | |
| Response | Explanation |
| y-1 |
Correct
|
| 24 | y is the 25th letter of alphabet, therefore 1 less is 24 |
| 1y | Whereas 10h means 10 more than h to some students, 1y means 1 less than y as in Roman numerals |
| Uw | Abbreviated words 'Unknown weight'. |
| x | Choose another letter or letter before y for Sue's weight. |
Teaching Strategies
As the study referred to above showed, misinterpretations of letters come from a natural process of students drawing on meanings from other contexts and prior learning to interpret the new language of algebra. In addition some misconceptions are taught.
Two teaching strategies lie behind the activities in this section. Firstly avoid teaching misconceptions. Secondly, be alert to misconceptions arising spontaneously as students try to make sense of new learning, so that experiences can be provided to address them quickly.
Activity 1: What’s my value of n? provides some suggestions for developing algebra with all students following through processes with their own numbers. Students recognise that a letter stands for a number, and that algebra laws are true for all numbers.
Activity 2: How many letters in my name? reinforces the notion of a letter as representing a number, not an object or an abbreviation. It introduces the concept that letters can be built up into sentences (expressions) in the same way as numbers.
Activity 3 provides some discussion items to increase students' awareness of common pitfalls at this level and above.
Activity 4 stresses that within one problem, an algebraic letter has only one meaning.
Activity 1: What’s my own value of n?
All introductory algebra activities need to reinforce that a letter stands for a number. Sometimes it is an unknown fixed number, sometimes a variable number, but always a number.
To teach algebra, it is often useful to have each student follow the processes with their own number. For example, in a lesson about 2(n + 3) = 2n + 6, it is helpful to have all students working out 2(n + 3) and 2n + 6 for different numbers. In this way, students can soon see that the two expressions are equal for many different numbers.
There are many easy ways to allocate personal numbers. Using the letter n to stand for the number of letters in their first name, students write down their value of n, e.g., Anna would write n = 4, Christopher would write n = 11. This can be extended to other contexts such as the number of legs of various animals, so students might choose a dog (n = 4) or a spider (n = 8) or an ant (n = 6).
Initially there is no harm in keeping to the letter n, as it reinforces the concept of the letter being a number. However, it is also important that students see that we can use any letter as long as we define it as a number, e.g. let a be the number of books in my locker.
Activity 2: How many letters in my name?
Once students have understood that a pronumeral stands for a number, simple expressions can be built up.
Example 1:
Let a = the number of letters in my first name.
Let b = the number of letters in my family name.
Altogether there are a + b letters in my name (students could include a third letter if they have a middle name).
So for Lini Marandri, a = 4, b = 8
So a + b = 4 + 8 = 12
For Thy Vo a = 3, b = 2
So a + b = 3 + 2 = 5
Ask student to write equations which are valid for their own names. For example Lini Marandri might write equations such as a + b +1 = 13 or a + a + 4 = b + 4 and Thy Vo might write b - a = 1 or a + a + a + 1 = b + 8 or 100 × (a + 1) = 400.
Have the equations checked by one friend and then pass the equations on slips of paper to the teacher, who writes them on the board without names. All students could then work out which equation belongs to which names. At this early stage, this is done by trial and error as an exercise in substitution, not equation solving. Students will observe that sometimes an equation could belong to several people. For example, b - a = 1 might belong to Thy Vo, or it might belong to Willie Wonka.
The key point is to emphasise that the algebraic letters (pronumerals) stand for numbers, and that equations are true for some numerical values of the pronumerals and not for others. Basic algebraic notation can be introduced during the lesson.
Example 2:
Let n = the number of students in the class.
How many shoes are there altogether?
Some students may say 2 × n while others may say n + n. By making n equal to the actual number of students in the classroom, for example, 23, students will see that these two different expressions are equivalent: 2 × 23 = 46 and 23 + 23 = 46.
How many toes are there altogether? (10n, or 10 × n - no need to omit the multiplication sign too early).
How many fingers? (10n)
What is the total number of fingers and toes? (10n + 10n = 20n)
In this class n = 23, so there are 20 × 23 fingers and toes. In the next door classroom, n = 21 so there are 20 × 21 fingers and toes.
In this way it will not take long for students to recognise that letters stand for numbers and that sometimes we can write algebraic expressions in a simpler way.
Using formulae in measurement
When using formulae in Measurement, it should be made clear to students that each letter stands for a number, not a number and a unit.
For example, let the perimeter be P cm, rather than let the perimeter be P. The letter P is standing for the number of centimetres in the perimeter.
Measurement formulae also provide a good means of linking with the concept of equivalent expressions. For example, when writing a Logo procedure in MicroWorlds to calculate the perimeter of a rectangle, students used two sliders that they called L and W to represent the number of turtle steps in the length and width. Some students used the programming P = L + L + W + W, whereas others used P = 2 * L + 2 * W. One student used P = 2 * (L + W). Each of the students knew that they were correct because their formula gave them the correct perimeter for their slider settings. This provided an opportunity for discussing the equivalence of these expressions, which then led naturally into a + a + b + b = 2a+ 2b = 2(a + b).
Activity 3: Confusions about the meanings of letters
The examples below illustrate some of the errors that students make when they are unclear about the meanings of algebraic letters and equations. At this level, it is important that students have a good introduction to algebra, stressing that the pronumerals (letters) stand for numbers and that equations say that two numbers are equal.
The following situations are worthwhile discussing carefully when they arise in class, during the first several years of learning algebra. These points will need to be revisited, since they have a tendency to spontaneously regenerate in students’ work. They may not arise at Level 4.25, although this provides the foundation.
(i) An apparent anomaly
When we write 1m = 100 cm, m and cm are used to stand for units - metres and centimetres. However, if we write an algebraic equation about the number of centimetres (c) in m metres, the equation is c = 100 m . In one case, the 100 is with the centimetres and in the other, it is with the metres.
The reason is that in one case m stands for the metre itself. In the other case m is used to stand for the number of metres. These are important distinctions.
(ii) A common error
Many students make errors like this. Asked to write an equation to describe with algebra, the situation
6 doughnuts cost $12
a student might write 6 d = 12 and read this equation by saying "6 doughnuts cost 12 dollars", pointing to the symbols as shown below. The equation is good, but it does not mean what the student says it means.
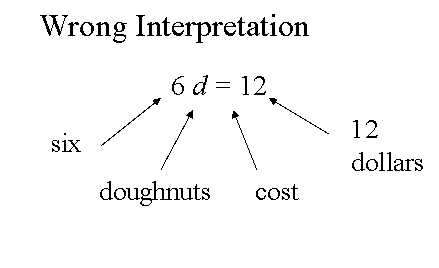
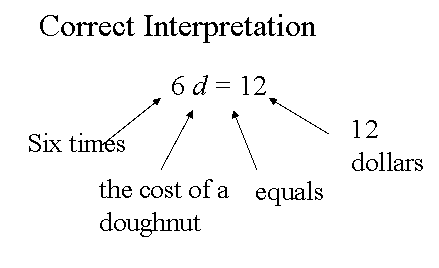
If this is an algebraic equation, the correct interpretation is "6 times the cost of a doughnut in dollars is equal to 12 dollars". d stands for the number of dollars, not the doughnut, which the student thinks.
Whenever students read equations using a verb other than 'equals' for '=', question them carefully about their meanings for letters.
This level of precision may sound pedantic, but errors of this type are a major cause of difficulty in many later applications (e.g. with linear programming in senior mathematics).
(iii) An infamous problem: deceptively simple
This is one of the most famous problems in mathematics education (Kieran, 1992). It is answered wrongly by many students (at all levels, including university) if they think about letters as abbreviations, or things, or as units and do not carefully think about the relationships between the numbers involved.
Let S stand for the number of students. Let P be the number of professors. Write an equation which says that there are 6 times as many students as professors.
The very common error is to write 6S = P, instead of the correct equation 6P =S. Since S is the larger number, there is a strong mental tendency for it to be associated in the equation with the 6 times. Students explaining their wrong equation 6S=P will probably not use the word ‘equals’.
To convince students, use a numerical example. If there are 100 professors, then there will be 600 students and 6 × 100 = 600. Students should learn to check their own equations with numbers – good checking skills are an essential part of Working Mathematically.
Activity 4: Algebraic letters have a fixed meaning within a problem
The concept of an unknown but fixed number, or of a variable, is difficult to convey in words. When students use algebra to solve problems, it is important that they write down clearly at the start of a problem what quantity each variable is standing for. In any one problem, one letter is allocated to one unknown quantity.
Below we show the type of error that students make in their subsequent use of algebra when they do not appreciate this fundamental principle. Teachers need to emphasise this principle from the start of algebra and frequently revisit it in subsequent years.
A Year 8 student, Les, was solving this problem:
Mark and Jan share $47 but Mark gets $5 more than Jan. How much do they each get?
Les knew that he would take $5 off $47, divide the remainder ($42) in 2 equal parts to get 2 lots of $21 and then increase Mark's amount by the initial $5. This is a good solution.
But how does Les think about this problem in algebra? He began by writing 5 + x = 47 and described his thinking to the interviewer this way:
Les: x is what is left out of $47 if you take $5 off it.
Interviewer: what might the x be?
Les: Say she gets $22 and he gets $27 (He hasn't found the answer of $21 at this stage, but guesses $22). They are sharing two x’s.
Interviewer: What are the two x’s?
Les: Unknowns…they are two different numbers, 22 and 27.
Interviewer: So what is this x? (pointing to 5 + x = 47)
Les: That was what was left over from $47, so its $42.
Les' good problem solving skills cannot connect with his algebra learning, because he thinks of x as any unknown quantity, rather than it representing one quantity throughout the problem. In his interview, he thinks about x as three quantities: $42, Jan's amount and Mark's amount.
Correct solution
A correct solution sets the meaning of the unknowns at the beginning of the problem, and keeps this one meaning through the problem. Insist that your students write down the meaning for unknowns before they begin a problem.
Let x be the number of dollars that Jan gets.
Mark then gets x + 5 dollars.
Together they have 47 dollars: x + (x + 5) = 47.
2x + 5 = 47
2x = 42
x = 21
Jan gets $21 and Mark gets $26.
References
Hart, K.M. (Ed.) Children's Understanding of Mathematics 11 - 16. John Murray, London.
Kieran, C. (1992). The Learning and Teaching of School Algebra, In D.A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 390-419). New York: Macmillan.
MacGregor, M. & Stacey, K. (1997). Students’ understanding of algebraic notation. Educational Studies in Mathematics, 33, 1 – 19.
Stacey, K.& MacGregor, M. (1997). Ideas about symbolism that students bring to algebra. The Mathematics Teacher, 90(2), 110 – 113.
